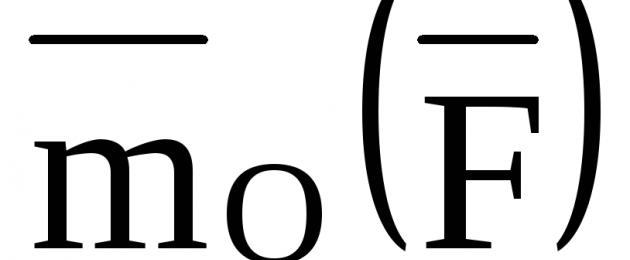När man betraktar ett rumsligt kraftsystem används begreppet kraftmoment i förhållande till centrum (eller punkt).

Definition. Kraftmomentet i förhållande till centrum O är vektorn som appliceras vid centrum O
, vars modul är lika med produkten av kraftens modul F genom sin skuldra h och som är riktad vinkelrätt mot planet som passerar genom centrum O och kraften, i den riktning från vilken kraften är synlig och tenderar att rotera kroppen runt mitten O moturs (fig. 17). Kraftens F arm h i förhållande till centrum O är längden på det vinkelräta segmentet sänkt från punkt O till kraftens verkningslinje.

Enligt denna definition

Kraftmomentet mäts i newtonmeter (Nm).

För att hitta formeln som uttrycker vektorn
, överväg vektorprodukten
. A-priory

Riktad vektor
vinkelrätt mot OAB-planet i den riktning från vilken den kortaste inriktningen
Med (om de är avsatta från en punkt) kan ses ske moturs, dvs. samma som vektor
. Därför vektorerna
Och uttrycka samma mängd. Härifrån

eller
, (12)

Var
– radievektor för punkt A ritad från centrum O.

Maktens ögonblick
har följande egenskaper:

1) kraftmomentet i förhållande till centrum kommer inte att ändras när kraftens appliceringspunkt flyttas längs dess verkningslinje;

2) kraftmomentet i förhållande till centrum O är lika med noll antingen när kraften är noll, eller när kraftens verkningslinje passerar genom centrum O (armen är noll).

§7. Algebraiskt kraftmoment om centrum

När man betraktar ett plan kraftsystem används begreppet algebraiskt kraftmoment i förhållande till centrum. När alla krafter i systemet ligger i ett plan är deras moment i förhållande till varje centrum O som ligger i samma plan vinkelräta mot detta plan, dvs. riktad längs samma räta linje. Sedan, utan att tillgripa vektorsymbolik, kan du skilja riktningarna för dessa ögonblick från varandra med ett tecken och överväga kraftögonblicket relativt centrum O som en algebraisk storhet. Låt oss komma överens om att kalla ett sådant ögonblick algebraiskt och beteckna det med symbolen
. Algebraiskt kraftmoment relativt centrum O är lika med produkten av kraftmodulen och dess skuldra tagen med motsvarande tecken, dvs.

. (13)

I detta fall anses momentet vara positivt när kraften tenderar att rotera kroppen runt mitten O moturs, och negativt när den roterar medurs. Så för krafterna som visas i fig. 18:
,
.

§8. Ett par krafter. Par ögonblick

Ett kraftpar är ett system av två lika stora, parallella och riktade i motsatta riktningar krafter som verkar på en absolut stel kropp (Fig. 19, a).

Force system ,, som bildar ett par, är inte i jämvikt (dessa krafter är inte riktade längs samma räta linje (axiom 1)). Samtidigt har kraftparet inte en resulterande kraft pga
. Därför bör egenskaperna hos ett kraftpar, som ett nytt oberoende element av statik, övervägas separat.

Planet som passerar genom kraftparets kraftlinjer kallas parets plan. Avståndet d mellan kraftparens verkningslinjer kallas parets axel. Verkan av ett par krafter på en stel kropp reduceras till en viss rotation parets ögonblick.

Definition: momentet för ett kraftpar är en vektor , vars modul är lika med produkten av modulen för en av krafterna i paret genom sin skuldra och som är riktad vinkelrätt mot parets verkningsplan i den riktning från vilken paret är synligt och försöker vända kropp moturs (fig. 19, b), dvs.

.

Till skillnad från kraftmomentet är vektorn för ett par en fri vektor, d.v.s. den kan bäras överallt på kroppen.

Momentet för ett par kan ges ett annat uttryck: momentet för ett par är lika med summan av momenten i förhållande till något centrum O av krafterna som bildar paret, d.v.s.

. (14)

För att bevisa detta, låt oss rita radievektorer från en godtycklig punkt O (Fig. 20)
Och
. Sedan, enligt formel (12), med hänsyn också till detta
, vi får

, och därför

Var
.

Därför att
, då är giltigheten av jämlikhet (14) bevisad. Härifrån följer i synnerhet resultatet som redan noterats ovan

eller
, (15)

de där. momentet för ett par är lika med momentet för en av dess krafter i förhållande till den andra kraftens appliceringspunkt. Låt oss också notera att modulen för momentet av paret

Av formel (14) följer att två kraftpar med samma moment är ekvivalenta.

Av formel (14) följer också att om en kropp påverkas av flera par med moment
,
, …,
då summan av momenten av alla krafter som bildar dessa par i förhållande till något centrum kommer att vara lika med
, och därför motsvarar hela uppsättningen av dessa par ett par med ett moment

. (17)

Detta resultat uttrycker satsen om addition av par.

System av två lika stora och parallella krafter, riktad mot motsatt fester och inte ligga på samma raka linje, ringde ett par krafter. Ett exempel på ett sådant kraftsystem är krafter som överförs från förarens händer till bilens ratt.

Power-paret har väldigt stor mening i praktiken. Det är därför egenskaper par som specifika åtgärder mekanisk interaktion mellan kroppar studeras separat.

Belopp parstyrkan är lika noll

P - P" = 0 (ris. A ),

dvs. ett kraftpar har ingen resultat. Trots detta är kroppen påverkad av ett par krafter är inte i balans.

Handling av ett par krafter på en fast kropp, som erfarenheten visar, är att den tenderar rotera det här är kroppen.

Förmågan hos ett kraftpar att producera rotation kvantitativt fast besluten ett par ögonblick, likvärdig produkt av kraft och kortaste avstånd(tagen från vinkelrät till styrka) mellan krafternas verkningslinjer.

Låt oss beteckna parets ögonblick M , och det kortaste avståndet mellan krafterna A , sedan det absoluta värdet av momentet (fig. A )

M = Ra = P "a .

Kortaste sträckan mellan krafternas verkningslinjer kallas axel par, så det kan vi säga ögonblick kraftpar är lika i absoluta värde produkten av en av krafterna i paret och dess skuldra.

Effekt verkan av ett par krafter fullt bestäms av dess ögonblick. Därför kan ett par krafter representeras bågformad pil, indikerar riktning rotation (se figur).

Eftersom ett kraftpar inte har en resultant, är det kan inte balanseras med enbart våld.

I International System of Units (SI) kraft mäts i newton, och axeln in meter. Respektive ögonblick par i systemet SI mätt i newtonometer (Nm) eller i enheter multiplar newtonometer: kn m, Mn m, etc.

Vi kommer att överväga ögonblicket för ett par krafter positiv, om paret tenderar att vända kroppen i medurs riktning(ris. A ) Och negativ, om paret tenderar att rotera kroppen moturs(ris. b ).

Godkänd teckenregel för momentpar villkorligt; kunde accepteras motsatt regel. När du löser problem, för att undvika förvirring, bör du alltid ta en specifik teckenregel.

Som ni vet är kraft det huvudsakliga måttet på interaktion mellan två kroppar. Låt oss på en fri kropp applicera två lika stora, motsatt riktade krafter som ligger på parallella räta linjer (Fig. 3.4). Huvudvektorn för detta kraftsystem är lika med noll, det vill säga den här kroppen kommer inte att röra sig framåt. Kommer det att vara i jämvikt? (Föreställ dig att du applicerade ett sådant kraftsystem på en vattenkran). Vilken rörelse kommer att starta??? Roterande. Det vill säga du måste ha mått på rotationsverkan ett sådant system med två krafter:

3.Moment av ett par krafter .

För att mäta den gemensamma rotationsverkan av krafterna i ett par och i förhållande till en godtycklig punkt HANDLA OM ( ris. 3.5) hitta summan av momenten för dessa krafter i förhållande till punkten HANDLA OM, kom ihåg formel (3.2):

, (3.3)

eller .

Denna vektor är vinkelrät mot kraftparets verkningsplan och är riktad dit det kan ses att parets rotation av kroppen sker moturs (fig. 3.6).

Storleken på vektormomentet (vektor - moment) för ett kraftpar, som modulen för vektorprodukten, är lika med Var α – vinkel mellan vektorer och (Fig. 3.6). Låt oss ange var d– parets axel.

Sedan . (3.4)

Om par av krafter är belägna i samma plan, så hittas storleken på deras moment enligt formel (3.4), och vektorerna för dessa moment kommer att vara kolinjära. I det här fallet är det mer ändamålsenligt att inte använda vektorbegreppet för momentet av ett kraftpar, utan algebraisk.

Maktens ögonblick. Ett par krafter.

1. Grundläggande begrepp och definitioner av statik.

Materialobjekt i statik:

material punkt,

system av materialpunkter,

absolut solid kropp.

Ett system av materialpunkter, eller ett mekaniskt system,är en samling av materialpunkter där varje punkts position och rörelse beror på positionen och rörelsen för andra punkter i detta system.

Absolut stel kroppär en kropp vars avstånd mellan två punkter inte ändras.

En fast kropp kan vara i vilotillstånd eller i rörelse av en viss karaktär. Vi kommer att ringa var och en av dessa stater kroppens kinematiska tillstånd.

	Tvinga- ett mått på den mekaniska växelverkan mellan kroppar, som bestämmer intensiteten och riktningen för denna växelverkan. Tvinga kan appliceras vid en punkt, då är denna kraft koncentrerad. Tvinga kan verka på alla punkter av en given volym eller yta av kroppen, då är denna kraft distribuerad.
	System av krafter - med helheten av krafter som verkar på en given kropp.
	Resulterande kallas en kraft som motsvarar ett visst kraftsystem.
	En balanserande kraft kallas en kraft lika stor som resultanten och riktad längs linjen för dess verkan i motsatt riktning.
	Ett system av ömsesidigt balanserande krafterär ett kraftsystem som, när det appliceras på en fast kropp i vila, inte tar bort den från detta tillstånd.

Inre krafter- dessa är krafter som verkar mellan punkter eller kroppar i ett givet system.

Yttre krafter- dessa är krafter som verkar från punkter eller kroppar som inte ingår i ett givet system.

Statiska uppgifter:

- omvandling av kraftsystem som verkar på en fast kropp till system likvärdiga med dem;

- studie av kroppars jämviktsförhållanden under påverkan av krafter som appliceras på dem.

1. Statikens axiom.

		3. Axiom för addition och uteslutning av balanserande krafter. Verkan av ett kraftsystem på en fast kropp kommer inte att förändras om ett system av ömsesidigt balanserande krafter läggs till eller utesluts från det. Följd. Utan att ändra det kinematiska tillståndet för en absolut stel kropp kan kraften överföras längs linjen för dess verkan, och hålla dess modul och riktning oförändrad. MED slam - glidande vektor.
	4. Axiom för parallellogram av krafter. Resultanten av två skärande krafter appliceras vid skärningspunkten och representeras av diagonalen av ett parallellogram konstruerat på dessa krafter.

5. Axiom för lika handling och reaktion. Varje handling har en lika och motsatt reaktion.

2. Samband och deras reaktioner

En stel kropp kallas fri om den kan röra sig i rymden i någon riktning.

En kropp som begränsar rörelsefriheten för en given stel kropp är en koppling i förhållande till den.

En stel kropp vars rörelsefrihet begränsas av bindningar kallas icke-fri.

Alla krafter som verkar på en icke-fri stel kropp kan delas in i:

• aktivera)
• bindningsreaktioner

Ställ in kraft uttrycker verkan på en given kropp av andra kroppar som kan orsaka en förändring i dess kinematiska tillstånd.

Kommunikationsreaktion - detta är den kraft med vilken en given anslutning verkar på kroppen och förhindrar en eller annan av dess rörelser.

Principen för befrielse av fasta ämnen från bindningar - en icke-fri fast kropp kan betraktas som en fri kropp, på vilken, förutom de specificerade krafterna, reaktioner av bindningar verkar.

Hur bestämmer man riktningen för en reaktion?

Om det finns två ömsesidigt vinkelräta riktningar på planet, i en av vilka anslutningen förhindrar kroppens rörelse, och i den andra inte, är riktningen för dess reaktion motsatt till den första riktningen.

I allmänhet kopplingens reaktion är riktad i motsatt riktning mot den där kopplingen inte tillåter kroppen att röra sig.

	Fast gångjärn Mobil

3. Kraftmoment runt mitten

Ett ögonblick av makt F i förhållande till något fast centrum O är en vektor placerad vinkelrätt mot planet som passerar genom kraftvektorn och centrum O riktad i den riktningen så att man från dess ände kan se kraftens rotation F relativt mitten O moturs.

Kraftmomentets egenskaper i förhållande till centrum:

	1) Kraftmomentets modul i förhållande till centrum kan uttryckas med dubbla arean av triangeln OAV (1.1) 2) Kraftmoment i förhållande till centrum lika med noll i händelse av att kraftens verkningslinje passerar genom denna punkt, dvs h = 0 .
	3) Om från en punkt HANDLA OM till punkten för tillämpning av våld A rita en radievektor, då kan vektorn för kraftmomentet uttryckas som en vektorprodukt (1.2)
	4) När en kraft överförs längs dess verkningslinje, förändras inte vektorn för dess moment relativt en given punkt.

Om flera krafter som ligger i samma plan appliceras på en stel kropp, kan du beräkna den algebraiska summan av momenten av dessa krafter i förhållande till vilken punkt som helst i detta plan

Ögonblick M O , lika med den algebraiska summan av momenten i ett givet system i förhållande till någon punkt i samma plan, kallas kraftsystemets huvudmoment i förhållande till denna punkt.

3. Kraftmoment runt axeln

För att bestämma kraftmomentet runt en axel måste du:

1) rita ett plan vinkelrätt mot Z-axeln;

2) bestämma punkten HANDLA OM skärning av en axel med ett plan;

3) projektera kraft ortogonalt F till detta plan;

4) hitta momentet för kraftprojektion F i förhållande till punkten O för skärningspunkten mellan axeln och planet.

Signera regel:

Kraftmomentet i förhållande till axeln anses positivt om man tittar mot Z-axeln , man kan se att projektionen tenderar att rotera planet jag runt Z-axeln i motsatt riktning mot medurs rotation.

Kraftmomentets egenskaper i förhållande till axeln 1) Kraftmomentet i förhållande till axeln representeras av ett segment plottat längs Z-axeln från punkt O i positiv riktning om > 0 och i negativ riktning om< 0. 2) Värdet på kraftmomentet runt axeln kan uttryckas med två gånger arean Δ (1.5) 3) Kraftmomentet i förhållande till axeln är noll i två fall: Om F 1 = 0, det vill säga kraftens verkningslinje är parallell med axeln; om h 1 = 0 , det vill säga kraftens verkningslinje skär axeln.

4. Kraftpar. Vektor och algebraiska moment av ett par krafter

Ett system med två lika stora, parallella och motsatt riktade krafter och kallas ett par krafter.

Planet där krafternas verkningslinjer och är belägna kallas aktionsplan för ett kraftpar.

Kortaste sträckan h mellan verkningslinjerna för krafterna som utgör paret kallas axeln av ett par krafter.

Moment av ett par krafter bestäms av produkten av modulen för en av krafterna i paret och skuldran.

Regel för tecken

Momentvektorn M för paret är riktad vinkelrätt mot kraftparets verkningsplan i en sådan riktning att man tittar mot denna vektor kan se kraftparet som tenderar att rotera dess verkningsplan i motsatt riktning till medurs rotation.

1. 4. Egenskaper för kraftpar på ett plan

Fastighet 1. Moment vektor M par i storlek och riktning är lika med vektorprodukten av vektorns radie AB till krafterna i detta par, mot vars början radievektorn är riktad AB, det är

(1.7)

Fastighet 2. Huvudmomentet för krafterna som utgör ett par i förhållande till en godtycklig punkt på parets verkningsplan beror inte på positionen för denna punkt och är lika med momentet för detta kraftpar.

5. Förutsättningar för ekvivalensen av kraftpar

Sats om villkoret för ekvivalens av kraftpar,

ligger i samma plan.

Med ett par krafterär ett system av två krafter lika stora, parallella och riktade i olika riktningar.

Låt oss betrakta kraftsystemet (R; B"), bildar ett par.

Ett par krafter orsakar rotation av kroppen och dess effekt på kroppen mäts av momentet. Krafterna som kommer in i paret är inte balanserade, eftersom de appliceras på två punkter (Fig. 4.1).

Deras verkan på kroppen kan inte ersättas av en kraft (resultant).

Momentet för ett kraftpar är numeriskt lika med produkten av kraftmodulen och avståndet mellan krafternas verkningslinjer (parets axel).

Momentet anses vara positivt om paret roterar kroppen medurs (fig. 4.1(b)):

M(F;F") = Fa; M > 0.

Planet som passerar genom kraftparets kraftlinjer kallas handlingsplan för paret.

Egenskaper för par(utan bevis):

1. Ett par krafter kan flyttas i dess verkningsplan.

2. Likvärdighet av par.

Två par vars moment är lika (fig. 4.2) är likvärdiga (deras effekt på kroppen är liknande).

3. Addering av kraftpar. Systemet med kraftpar kan ersättas av ett resulterande par.

Momentet för det resulterande paret är lika med den algebraiska summan av momenten för de par som utgör systemet (fig. 4.3):

4. Jämvikt av par.

För jämvikt av par är det nödvändigt och tillräckligt att den algebraiska summan av momenten i systemets par är lika med noll:

Slut på arbetet -

Detta ämne hör till avsnittet:

Teoretisk mekanik

Teoretisk mekanik.. föreläsning.. ämne: statikens grundläggande begrepp och axiom..

Om du behöver ytterligare material om detta ämne, eller om du inte hittade det du letade efter, rekommenderar vi att du använder sökningen i vår databas med verk:

Vad ska vi göra med det mottagna materialet:

Om detta material var användbart för dig kan du spara det på din sida på sociala nätverk:

Tweet

Alla ämnen i detta avsnitt:

Problem med teoretisk mekanik
Teoretisk mekanik är vetenskapen om den mekaniska rörelsen av materiella fasta kroppar och deras interaktion. Mekanisk rörelse förstås som en kropps rörelse i rum och tid från

Tredje axiomet
Utan att störa kroppens mekaniska tillstånd kan du lägga till eller ta bort ett balanserat kraftsystem (principen att kassera ett kraftsystem som motsvarar noll) (Fig. 1.3). P,=P2P,=P.

Följd av andra och tredje axiomen
Kraften som verkar på en solid kropp kan flyttas längs linjen för dess verkan (Fig. 1.6).

Anslutningar och reaktioner av anslutningar
Alla statiska lagar och teorem är giltiga för en fri stel kropp. Alla kroppar är indelade i fria och bundna. Fria kroppar är kroppar vars rörelse inte är begränsad.

Hård spö
I diagrammen är stavarna avbildade som en tjock heldragen linje (Fig. 1.9). Spöet kan

Fast gångjärn
Fästpunkten kan inte flyttas. Stången kan rotera fritt runt gångjärnsaxeln. Reaktionen av ett sådant stöd passerar genom gångjärnsaxeln, men

Plansystem av konvergerande krafter
Ett kraftsystem vars verkningslinjer skär varandra vid en punkt kallas konvergent (fig. 2.1).

Resultatet av konvergerande krafter
Resultanten av två skärande krafter kan bestämmas med hjälp av ett parallellogram eller krafttriangel (4:e axiom) (vis. 2.2).

Jämviktstillstånd för ett plan system av konvergerande krafter
När kraftsystemet är i jämvikt måste resultanten vara lika med noll, därför måste, i en geometrisk konstruktion, slutet av den sista vektorn sammanfalla med början av den första. Om

Lösa jämviktsproblem med en geometrisk metod
Det är bekvämt att använda den geometriska metoden om det finns tre krafter i systemet. När du löser jämviktsproblem, betrakta kroppen som absolut solid (stelnad). Procedur för att lösa problem:

Lösning
1. Krafterna som uppstår i fäststängerna är lika stora som de krafter med vilka stängerna stödjer belastningen (5:e axiom för statik) (Fig. 2.5a). Vi bestämmer möjliga reaktionsriktningar pga

Projektion av kraft på axeln
Kraftprojektionen på axeln bestäms av axelsegmentet, avskuret av perpendikulära sidor som sänks ner på axeln från början och slutet av vektorn (fig. 3.1).

Styrka på ett analytiskt sätt
Storleken på resultanten är lika med vektorns (geometriska) summa av kraftsystemets vektorer. Vi bestämmer resultatet geometriskt. Låt oss välja ett koordinatsystem, bestämma projektionerna för alla uppgifter

Konvergerande krafter i analytisk form
Baserat på det faktum att resultanten är noll får vi: Tillstånd

Kraftmoment ungefär en punkt
En kraft som inte passerar genom kroppens fästpunkt orsakar rotation av kroppen i förhållande till punkten, därför uppskattas effekten av en sådan kraft på kroppen som ett moment. Kraftmoment rel.

Poinsots sats om parallell överföring av krafter
En kraft kan överföras parallellt med linjen för dess verkan; i detta fall är det nödvändigt att lägga till ett par krafter med ett moment lika med produkten av kraftmodulen och avståndet över vilket kraften överförs.

Fördelade krafter
Verkningslinjerna för ett godtyckligt kraftsystem skärs inte vid en punkt, därför bör ett sådant system förenklas för att bedöma kroppens tillstånd. För att göra detta överförs alla krafter i systemet till en godtyckligt

Inverkan av referenspunkt
Referenspunkten väljs godtyckligt. När referenspunktens position ändras kommer värdet på huvudvektorn inte att ändras. Storleken på huvudmomentet när reduktionspunkten flyttas kommer att ändras,

Platt kraftsystem
1. Vid jämvikt är systemets huvudvektor noll. Analytisk bestämning av huvudvektorn leder till slutsatsen:

Typer av laster
Enligt appliceringsmetoden delas laster in i koncentrerade och fördelade. Om den faktiska lastöverföringen sker på ett försumbart litet område (vid en punkt) kallas lasten koncentrerad

Kraftmoment runt axeln
Kraftmomentet i förhållande till axeln är lika med kraftens projiceringsmoment på ett plan vinkelrätt mot axeln, i förhållande till axelns skärningspunkt med planet (fig. 7.1 a). MU

Vektor i rymden
I rymden projiceras kraftvektorn på tre ömsesidigt vinkelräta koordinataxlar. Vektorns projektioner bildar kanterna på en rektangulär parallellepiped, kraftvektorn sammanfaller med diagonalen (fig. 7.2)

Rumsligt konvergent kraftsystem
Ett rumsligt konvergent kraftsystem är ett kraftsystem som inte ligger i samma plan, vars verkningslinjer skär varandra vid en punkt. Resultatet av det rumsliga systemet

Att föra ett godtyckligt rumsligt kraftsystem till centrum O
Ett rumsligt kraftsystem ges (Fig. 7.5a). Låt oss ta det till mitten O. Krafterna måste flyttas parallellt, och ett system av kraftpar bildas. Momentet för vart och ett av dessa par är lika

Tyngdpunkten för homogena platta kroppar
(platta figurer) Mycket ofta är det nödvändigt att bestämma tyngdpunkten för olika platta kroppar och geometriska platta figurer med komplex form. För platta kroppar kan vi skriva: V =

Bestämma koordinaterna för tyngdpunkten för plana figurer
Notera. Tyngdpunkten för en symmetrisk figur ligger på symmetriaxeln. Spöets tyngdpunkt är mitt på höjden. Positionerna för tyngdpunkterna för enkla geometriska figurer kan

Kinematik för en punkt
Ha en uppfattning om rum, tid, bana, väg, hastighet och acceleration. Vet hur man specificerar en punkts rörelse (naturlig och koordinat). Känna till beteckningarna

Distans rest
Banan mäts längs banan i färdriktningen. Beteckning - S, måttenheter - meter. En punkts rörelseekvation: Ekvationsdefinierande

Hastighet
Den vektormängd som för närvarande kännetecknar hastigheten och rörelseriktningen längs banan kallas hastighet. Hastighet är en vektor riktad när som helst mot

Punktacceleration
En vektormängd som kännetecknar hastighetsändringen i storlek och riktning kallas en punkts acceleration. Punktens hastighet när du flyttar från punkt M1

Enhetlig rörelse
Enhetlig rörelse är rörelse med konstant hastighet: v = konst. För rätlinjig jämn rörelse (bild 10.1 a)

Lika växlande rörelse
Lika variabel rörelse är rörelse med konstant tangentiell acceleration: vid = konst. För rätlinjig enhetlig rörelse

Framåtrörelse
Translationell är rörelsen av en stel kropp där varje rak linje på kroppen under rörelse förblir parallell med dess initiala position (fig. 11.1, 11.2). På

Roterande rörelse
Under rotationsrörelse beskriver alla punkter på kroppen cirklar runt en gemensam fast axel. Den fasta axeln runt vilken kroppens alla punkter roterar kallas rotationsaxeln.

Speciella fall av rotationsrörelse
Uniform rotation (vinkelhastigheten är konstant): ω =const Ekvationen (lagen) för enhetlig rotation har i detta fall formen:

Hastigheter och accelerationer för punkter i en roterande kropp
Kroppen roterar runt punkt O. Låt oss bestämma rörelseparametrarna för punkt A, belägen på ett avstånd RA från rotationsaxeln (fig. 11.6, 11.7). Väg

Lösning
1. Sektion 1 - ojämn accelererad rörelse, ω = φ’; ε = ω’ 2. Sektion 2 - hastigheten är konstant - rörelsen är likformig, . ω = konst 3.

Grundläggande definitioner
En komplex rörelse är en rörelse som kan delas upp i flera enkla. Enkla rörelser anses vara translationella och roterande. Att överväga den komplexa rörelsen av punkter

Planparallell rörelse av en stel kropp
Planparallell, eller platt, rörelse av en stel kropp kallas sådan att alla punkter på kroppen rör sig parallellt med någon fast rörelse i referenssystemet i fråga.

Translationell och roterande
Planparallell rörelse delas upp i två rörelser: translationell med en viss pol och rotation i förhållande till denna pol. Nedbrytning används för att bestämma

Hastighetscenter
Hastigheten för vilken punkt som helst på kroppen kan bestämmas med hjälp av det momentana hastighetscentrumet. I detta fall representeras komplex rörelse i form av en kedja av rotationer runt olika centra. Uppgift

Dynamikens axiom
Dynamikens lagar generaliserar resultaten av många experiment och observationer. Dynamikens lagar, som vanligtvis betraktas som axiom, formulerades av Newton, men den första och fjärde lagen var också

Begreppet friktion. Typer av friktion
Friktion är det motstånd som uppstår när en grov kropp rör sig över ytan på en annan. När kroppar glider uppstår glidfriktion och när de rullar uppstår rullfriktion. Naturstöd

Rullande friktion
Rullmotståndet är förknippat med ömsesidig deformation av jorden och hjulet och är betydligt mindre än glidfriktion. Vanligtvis anses jorden vara mjukare än hjulet, då är jorden huvudsakligen deformerad, och

Gratis och icke-gratis poäng
En materiell punkt vars rörelse i rymden inte begränsas av några förbindelser kallas fri. Problem löses med hjälp av dynamikens grundläggande lag. Material då

Tröghetskraft
Tröghet är förmågan att behålla sitt tillstånd oförändrat; detta är en inre egenskap hos alla materiella kroppar. Tröghetskraft är en kraft som uppstår under acceleration eller inbromsning av kroppar

Lösning
Aktiva krafter: drivkraft, friktionskraft, gravitation. Reaktion i stödet R. Vi applicerar tröghetskraften i motsatt riktning från accelerationen. Enligt d'Alemberts princip, systemet av krafter som verkar på plattformen

Arbete utfört av resulterande kraft
Under inverkan av ett kraftsystem förflyttas en punkt med massan m från position M1 till position M 2 (Fig. 15.7). Vid rörelse under påverkan av ett kraftsystem, använd

Kraft
För att karakterisera arbetets prestanda och hastighet introducerades begreppet makt. Effekt - arbete utfört per tidsenhet:

Roterande kraft
Ris. 16.2 Kroppen rör sig längs en båge med radie från punkt M1 till punkt M2 M1M2 = φr kraftarbete

Effektivitet
Varje maskin och mekanism, när de utför arbete, spenderar en del av sin energi för att övervinna skadliga motstånd. Således utför maskinen (mekanismen), förutom nyttigt arbete, även ytterligare arbete.

Momentum change theorem
En materialpunkts rörelsemängd är en vektorkvantitet lika med produkten av punktens massa och dess hastighet mv. Vektorn av momentum sammanfaller med

Sats om förändringen av kinetisk energi
Energi är en kropps förmåga att utföra mekaniskt arbete. Det finns två former av mekanisk energi: potentiell energi, eller positionsenergi, och kinetisk energi.

Grunderna i dynamiken i ett system av materiella punkter
En uppsättning materialpunkter sammankopplade av interaktionskrafter kallas ett mekaniskt system. Varje materialkropp inom mekanik betraktas som en mekanisk

Grundläggande ekvation för dynamiken i en roterande kropp
Låt en stel kropp, under inverkan av yttre krafter, rotera runt Oz-axeln med vinkelhastighet

Spänningar
Sektionsmetoden gör det möjligt att bestämma värdet av den inre kraftfaktorn i en sektion, men gör det inte möjligt att fastställa lagen för fördelning av inre krafter över sektionen. För att bedöma styrkan hos n

Inre kraftfaktorer, spänningar. Konstruktion av diagram
Ha en uppfattning om längsgående krafter och normalspänningar i tvärsnitt. Känna till reglerna för att konstruera diagram över längsgående krafter och normalspänningar, fördelningslagen

Längsgående krafter
Låt oss betrakta en balk laddad med yttre krafter längs sin axel. Balken är fixerad i väggen (fäst "fixering") (Fig. 20.2a). Vi delar upp balken i lastområden. Lastyta med

Geometriska egenskaper hos plana sektioner
Ha en uppfattning om den fysiska innebörden och proceduren för att bestämma axiella, centrifugala och polära tröghetsmoment, de centrala huvudaxlarna och de viktigaste centrala tröghetsmomenten.

Statiskt moment för tvärsnittsarea
Låt oss överväga ett godtyckligt avsnitt (Fig. 25.1). Om vi ​​delar upp sektionen i infinitesimala areor dA och multiplicerar varje area med avståndet till koordinataxeln och integrerar den resulterande

Centrifugalt tröghetsmoment
Det centrifugala tröghetsmomentet för en sektion är summan av produkterna av elementära områden som tagits över båda koordinaterna:

Axiella tröghetsmoment
Det axiella tröghetsmomentet för en sektion i förhållande till en viss gård som ligger i samma plan kallas summan av produkterna av elementära områden som tagits över hela arean med kvadraten på deras avstånd

Sektionens polära tröghetsmoment
Det polära tröghetsmomentet för en sektion i förhållande till en viss punkt (pol) är summan av produkterna av elementära områden som tagits över hela arean med kvadraten på deras avstånd till denna punkt:

Tröghetsmoment av de enklaste sektionerna
Axiella tröghetsmoment för en rektangel (Fig. 25.2) Föreställ dig direkt

Polärt tröghetsmoment i en cirkel
För en cirkel, beräkna först det polära tröghetsmomentet, sedan de axiella. Låt oss föreställa oss en cirkel som en samling oändligt tunna ringar (bild 25.3).

Torsionsdeformation
Torsion av en rund balk uppstår när den belastas med kraftpar med moment i plan vinkelräta mot längdaxeln. I detta fall böjs strålens generatriser och roteras genom en vinkel γ,

Hypoteser för torsion
1. Hypotesen om plana sektioner är uppfylld: tvärsnittet av balken, platt och vinkelrät mot den längsgående axeln, efter deformation förblir platt och vinkelrät mot den längsgående axeln.

Interna kraftfaktorer under vridning
Torsion är en belastning där endast en inre kraftfaktor uppträder i balkens tvärsnitt - vridmoment. Externa belastningar är också två

Vridmomentdiagram
Momentmoment kan variera längs balkens axel. Efter att ha bestämt värdena för momenten längs sektionerna, konstruerar vi en graf över vridmomenten längs strålens axel.

Vridstress
Vi ritar ett rutnät av längsgående och tvärgående linjer på strålens yta och överväger mönstret som bildas på ytan efter Fig. 27.1a deformation (Fig. 27.1a). Pop

Maximala vridspänningar
Av formeln för bestämning av spänningar och diagrammet över fördelningen av tangentiella spänningar under torsion framgår att de maximala spänningarna uppstår på ytan. Låt oss bestämma den maximala spänningen

Typer av hållfasthetsberäkningar
Det finns två typer av hållfasthetsberäkningar: 1. Designberäkning - diametern på balken (axeln) i den farliga sektionen bestäms:

Styvhetsberäkning
Vid beräkning av styvhet bestäms deformationen och jämförs med den tillåtna. Låt oss betrakta deformationen av en rund balk under verkan av ett yttre kraftpar med ett moment t (fig. 27.4).

Grundläggande definitioner
Böjning är en typ av belastning där en intern kraftfaktor – ett böjmoment – ​​uppträder i balkens tvärsnitt. Timmer arbetar på

Interna kraftfaktorer vid böjning
Exempel 1. Betrakta en balk som påverkas av ett par krafter med ett moment m och en yttre kraft F (Fig. 29.3a). För att bestämma interna kraftfaktorer använder vi metoden med

Böjande ögonblick
En tvärkraft i en sektion anses vara positiv om den tenderar att rotera den

Differentiella beroenden för direkt tvärböjning
Konstruktionen av diagram över skjuvkrafter och böjmoment förenklas avsevärt genom att använda differentialförhållanden mellan böjmomentet, skjuvkraften och enhetlig intensitet

Använda sektionsmetoden Det resulterande uttrycket kan generaliseras
Tvärkraften i den aktuella sektionen är lika med den algebraiska summan av alla krafter som verkar på balken fram till den aktuella sektionen: Q = ΣFi Eftersom vi pratar

Spänningar
Låt oss betrakta böjningen av en balk som är klämd åt höger och belastad med en koncentrerad kraft F (Fig. 33.1).

Stresstillstånd vid en punkt
Det stressade tillståndet vid en punkt kännetecknas av normala och tangentiella spänningar som uppstår på alla områden (sektioner) som passerar genom denna punkt. Vanligtvis räcker det att bestämma till exempel

Konceptet med ett komplext deformerat tillstånd
Uppsättningen av deformationer som uppstår i olika riktningar och i olika plan som passerar genom en punkt bestämmer det deformerade tillståndet vid denna punkt. Komplex deformation

Beräkning av en rund balk för böjning med vridning
Vid beräkning av en rund balk under inverkan av böjning och torsion (fig. 34.3) är det nödvändigt att ta hänsyn till normala och tangentiella spänningar, eftersom de maximala spänningsvärdena i båda fallen uppstår

Begreppet stabil och instabil jämvikt
Relativt korta och massiva stavar är designade för kompression, eftersom de misslyckas till följd av förstörelse eller kvarvarande deformationer. Långa spön med litet tvärsnitt för action

Stabilitetsberäkning
Stabilitetsberäkningen består av att bestämma den tillåtna tryckkraften och, i jämförelse med den, den verkande kraften:

Beräkning med Eulers formel
Problemet med att bestämma den kritiska kraften löstes matematiskt av L. Euler 1744. För en stång med gångjärn på båda sidor (Fig. 36.2) har Eulers formel formen

Kritiska påfrestningar
Kritisk spänning är den tryckspänning som motsvarar den kritiska kraften. Spänningen från tryckkraften bestäms av formeln

Tillämpningsgränser för Eulers formel
Eulers formel är endast giltig inom gränserna för elastiska deformationer. Sålunda måste den kritiska spänningen vara mindre än materialets elasticitetsgräns. Föreg