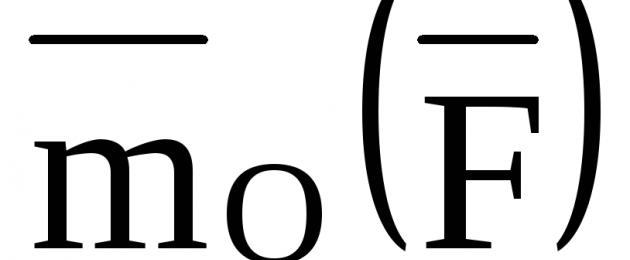Nagrinėjant erdvinę jėgų sistemą, naudojama jėgos momento centro (arba taško) atžvilgiu sąvoka.

Apibrėžimas. Jėgos momentas centro O atžvilgiu yra vektorius, taikomas centre O
, kurio modulis lygus jėgos modulio F sandaugai iš peties h ir kuris yra nukreiptas statmenai plokštumai, einančia per centrą O ir jėgai, ta kryptimi, iš kurios matoma jėga, linkusi suktis. korpusas aplink centrą O prieš laikrodžio rodyklę (17 pav.). Jėgos F petys h centro O atžvilgiu yra statmenos atkarpos, nuleistos nuo taško O iki jėgos veikimo linijos, ilgis.

Pagal šį apibrėžimą

Jėgos momentas matuojamas niutonmetrais (Nm).

Norėdami rasti formulę, kuri išreiškia vektorių
, apsvarstykite vektorinį sandaugą
. A-prioras

Nukreiptas vektorius
statmenai OAB plokštumai ta kryptimi, nuo kurios trumpiausias išlygiavimas
Su (jei jie atidėti iš vieno taško) gali būti matomi vykstantys prieš laikrodžio rodyklę, t.y. toks pat kaip vektorius
. Todėl vektoriai
Ir išreikšti tą patį kiekį. Iš čia

arba
, (12)

Kur
– taško A spindulio vektorius, nubrėžtas iš centro O.

Galios akimirka
turi šias savybes:

1) jėgos momentas centro atžvilgiu nepasikeis, kai jėgos taikymo taškas perkeliamas išilgai jo veikimo linijos;

2) jėgos momentas centro O atžvilgiu lygus nuliui arba kai jėga lygi nuliui, arba kai jėgos veikimo linija eina per centrą O (ranka lygi nuliui).

§7. Algebrinis jėgos momentas apie centrą

Nagrinėjant plokštuminę jėgų sistemą, naudojama algebrinio jėgos momento centro atžvilgiu sąvoka. Kai visos sistemos jėgos yra vienoje plokštumoje, jų momentai bet kurio toje pačioje plokštumoje esančio centro O atžvilgiu yra statmeni šiai plokštumai, t.y. nukreiptas išilgai tos pačios tiesios linijos. Tada, nesinaudodami vektorine simbolika, galite atskirti šių momentų kryptis vieną nuo kitos pagal ženklą ir atsižvelgti į jėgos momentą. centro O atžvilgiu kaip algebrinį dydį. Sutikime tokį momentą pavadinti algebriniu ir pažymėti simboliu
. Algebrinis jėgos momentas centro atžvilgiu O lygi jėgos modulio ir jo peties sandaugai, paimtai su atitinkamu ženklu, t.y.

. (13)

Šiuo atveju momentas laikomas teigiamu, kai jėga linkusi pasukti kūną aplink centrą O prieš laikrodžio rodyklę, ir neigiamu, kai jis sukasi pagal laikrodžio rodyklę. Taigi jėgoms, parodytoms Fig. 18:
,
.

§8. Pora jėgų. Pora akimirka

Jėgų pora – dviejų vienodo dydžio, lygiagrečių ir priešingomis kryptimis nukreiptų jėgų, veikiančių absoliučiai standų kūną, sistema (19 pav., a).

Jėgos sistema ,, sudarantis porą, nėra pusiausvyroje (šios jėgos nukreiptos ne išilgai tos pačios tiesės (aksioma 1)). Tuo pačiu metu jėgų pora neturi rezultatinės jėgos, nes
. Todėl jėgų poros, kaip naujo nepriklausomo statikos elemento, savybes reikėtų nagrinėti atskirai.

Plokštuma, einanti per poros jėgų veikimo linijas, vadinama poros plokštuma. Atstumas d tarp poros jėgų veikimo linijų vadinamas poros pečių. Jėgų poros veikimas standžiam kūnui sumažinamas iki tam tikro sukimosi poros akimirka.

Apibrėžimas: jėgų poros momentas yra vektorius , kurio modulis yra lygus vienos iš poros jėgų modulio sandaugai iš jos peties ir kuris yra nukreiptas statmenai poros veikimo plokštumai ta kryptimi, iš kurios matoma pora, bandanti pasukti korpusas prieš laikrodžio rodyklę (19 pav., b), t.y.

.

Skirtingai nuo jėgos momento, poros vektorius yra laisvasis vektorius, t.y. jį galima nešiotis bet kurioje kūno vietoje.

Poros momentui galima suteikti kitą išraišką: poros momentas lygus momentų sumai bet kurio porą sudarančių jėgų centro O atžvilgiu, t.y.

. (14)

Norėdami tai įrodyti, nubrėžkime spindulio vektorius iš savavališko taško O (20 pav.)
Ir
. Tada pagal (12) formulę, atsižvelgiant ir į tai
, mes gauname

, ir todėl

Kur
.

Nes
, tada lygybės (14) pagrįstumas yra įrodytas. Iš čia visų pirma seka aukščiau jau minėtas rezultatas

arba
, (15)

tie. poros momentas lygus vienos iš jos jėgų momentui kitos jėgos taikymo taško atžvilgiu. Taip pat atkreipkime dėmesį į tai, kad poros momento modulis

Iš (14) formulės išplaukia, kad dvi jėgų poros, turinčios vienodus momentus, yra lygiavertės.

Iš (14) formulės taip pat išplaukia, kad jei kūną veikia kelios poros su momentais
,
, …,
tada visų šias poras sudarančių jėgų momentų suma bet kurio centro atžvilgiu bus lygi
, todėl visas šių porų rinkinys yra lygiavertis vienai porai su momentu

. (17)

Šis rezultatas išreiškia porų sudėjimo teoremą.

Dviejų lygiagrečių ir lygiagrečių jėgų sistema, siekiama priešingas vakarėliams ir guli ne ant tos pačios tiesios linijos, paskambino pora jėgų. Tokios jėgų sistemos pavyzdys yra jėgų, perduodamų iš vairuotojo rankų į automobilio vairą.

Galios pora turi labai didelis prasmę praktikoje. Štai kodėl savybių poros kaip konkrečios priemones tiriama mechaninė kūnų sąveika atskirai.

Suma poros stiprumas yra vienodas nulis

P - P" = 0 (ryžiai. A ),

t.y. jėgų pora neturi rezultato. Nepaisant to, kūnas yra veikiamas kelių jėgų nėra pusiausvyroje.

Poros jėgų veikimas ant kieto kūno, kaip rodo patirtis, jis linkęs pasukti tai yra kūnas.

Jėgų poros gebėjimas sukelti sukimąsi kiekybiškai Atkaklus pora akimirka, lygus jėgos ir trumpiausio atstumo sandauga(paimta iš statmenaiį jėgą) tarp jėgų veikimo linijų.

Pažymėkime poros momentą M , ir trumpiausias atstumas tarp jėgų A , tada absoliuti momento vertė (pav. A )

M = Ra = P "a .

Trumpiausias atstumas tarp jėgų veikimo linijų vadinama pečių porų, todėl galime taip sakyti momentas jėgų poros yra lygios absoliučia verte vienos iš poros jėgų ir jos peties produktas.

Efektas poros jėgų veikimas pilnai lemia jos momentas. Todėl galima atstovauti porai jėgų lankinė rodyklė, nurodant kryptis sukimasis (žr. pav.).

Kadangi jėgų pora neturi rezultato, tai negali būti subalansuotas vien jėga.

IN Tarptautinė vienetų sistema (SI) jėga matuojama niutonų, o petys į vidų metrų. Atitinkamai momentas porų sistemoje SI matuojama niutonometrais (Nm) arba vienetais kartotiniai niutonometras: kn m, Mn m ir kt.

Mes apsvarstysime poros jėgų momentą teigiamas, jei pora linkusi apversti kūną pagal laikrodžio rodyklę(ryžiai. A ) Ir neigiamas, jei pora linkusi sukti kūną prieš laikrodžio rodyklę(ryžiai. b ).

Priimta ženklų taisyklė momentų poroms sąlyginai; galėtų būti priimtas priešingas taisyklė. Spręsdami problemas, kad išvengtumėte painiavos, visada turėtumėte imtis vienos konkrečios ženklo taisyklės.

Kaip žinote, jėga yra pagrindinis dviejų kūnų sąveikos matas. Laisvajam kūnui taikykime dvi vienodo dydžio, priešingai nukreiptas jėgas, esančias lygiagrečiose tiesėse (3.4 pav.). Pagrindinis šios jėgų sistemos vektorius yra lygus nuliui, tai yra, šis kūnas nejudės į priekį. Ar bus pusiausvyra? (Įsivaizduokite, kad tokią jėgų sistemą pritaikėte vandens čiaupui). Koks judėjimas prasidės??? Rotacinis. Tai yra, jūs turite turėti sukimosi veiksmo matas tokia dviejų jėgų sistema:

3.Poros jėgų akimirka .

Išmatuoti bendrą poros jėgų sukimosi veiksmą savavališko taško atžvilgiu APIE ( ryžių. 3.5) raskite šių jėgų momentų sumą taško atžvilgiu APIE, prisimindamas (3.2) formulę:

, (3.3)

arba .

Šis vektorius yra statmenas jėgų poros veikimo plokštumai ir nukreiptas ten, kur matyti, kad kūno sukimasis pora vyksta prieš laikrodžio rodyklę (3.6 pav.).

Jėgų poros vektorinio momento (vektoriaus – momento) dydis, kaip vektoriaus sandaugos modulis, yra lygus Kur α – kampas tarp vektorių ir (3.6 pav.). Pažymėkime kur d– poros petys.

Tada . (3.4)

Jei jėgų poros yra toje pačioje plokštumoje, tada jų momentų dydžiai nustatomi pagal (3.4) formulę, o šių momentų vektoriai bus kolinearūs. Šiuo atveju tikslingiau naudoti ne vektorinę jėgų poros momento sampratą, o algebrinė.

Galios akimirka. Pora jėgų.

1. Pagrindinės statikos sąvokos ir apibrėžimai.

Materialūs objektai statikoje:

materialus taškas,

materialių taškų sistema,

visiškai tvirtas kūnas.

Medžiagų taškų sistema arba mechaninė sistema, yra materialių taškų rinkinys, kuriame kiekvieno taško padėtis ir judėjimas priklauso nuo kitų šios sistemos taškų padėties ir judėjimo.

Absoliučiai tvirtas korpusas yra kūnas, kurio atstumas tarp dviejų taškų nekinta.

Tvirtas kūnas gali būti ramybės būsenoje arba tam tikro pobūdžio judėjime. Kiekvieną iš šių valstybių vadinsime kinematinė kūno būklė.

	Jėga- kūnų mechaninės sąveikos matas, nustatantis šios sąveikos intensyvumą ir kryptį. Jėga gali būti taikoma taške, tada ši jėga yra koncentruotas. Jėga gali veikti visus tam tikro kūno tūrio ar paviršiaus taškus, tada ši jėga yra platinami.
	Jėgų sistema – su duotą kūną veikiančių jėgų visuma.
	Rezultatas vadinama jėga, lygiaverte tam tikrai jėgų sistemai.
	Balansuojanti jėga vadinama jėga, kurios dydis yra lygus rezultatui ir nukreiptas išilgai jos veikimo linijos priešinga kryptimi.
	Tarpusavio pusiausvyros jėgų sistema yra jėgų sistema, kuri, veikiama ramybės būsenos kietam kūnui, nepašalina jo iš šios būsenos.

Vidinės jėgos- tai jėgos, veikiančios tarp tam tikros sistemos taškų ar kūnų.

Išorinės jėgos- tai jėgos, veikiančios iš taškų ar kūnų, kurie nėra tam tikros sistemos dalis.

Statikos užduotys:

- kietą kūną veikiančių jėgų sistemų transformavimas į joms lygiavertes sistemas;

- kūnų, veikiančių juos veikiančių jėgų, pusiausvyros sąlygų tyrimas.

1. Statikos aksiomos.

		3. Balansuojančių jėgų pridėjimo ir išskyrimo aksioma. Jėgų sistemos veikimas kietam kūnui nepasikeis, jei prie jo bus pridėta arba iš jos neįtraukta tarpusavyje balansuojančių jėgų sistema. Pasekmė. Nekeičiant absoliučiai standaus kūno kinematinės būsenos, jėga gali būti perkelta išilgai jo veikimo linijos, išlaikant nepakitusią modulį ir kryptį. SU dumblas - slenkantis vektorius.
	4. Jėgų lygiagretainio aksioma. Dviejų susikertančių jėgų rezultatas taikomas jų susikirtimo taške ir yra pavaizduotas lygiagretainio, sudaryto iš šių jėgų, įstrižainės.

5. Veiksmo ir reakcijos lygybės aksioma. Kiekvienas veiksmas turi lygią ir priešingą reakciją.

2. Ryšiai ir jų reakcijos

Kietas kūnas vadinamas laisvuoju, jei jis gali judėti erdvėje bet kuria kryptimi.

Kūnas, ribojantis tam tikro standaus kūno judėjimo laisvę, yra ryšys su juo.

Kietas kūnas, kurio judėjimo laisvę riboja saitai, vadinamas nelaisvu.

Visas jėgas, veikiančias nelaisvą standųjį kūną, galima suskirstyti į:

• nustatyti (aktyvus)
• ryšių reakcijos

Nustatykite jėgą išreiškia kitų kūnų veikimą, galintį pakeisti jo kinematinę būseną.

Bendravimo reakcija - tai jėga, kuria tam tikras ryšys veikia kūną, užkertant kelią vienam ar kitam jo judesiui.

Kietųjų dalelių išlaisvinimo iš jungčių principas - nelaisvas kietas kūnas gali būti laikomas laisvu kūnu, kuriame, be nurodytų jėgų, veikia ryšių reakcijos.

Kaip nustatyti reakcijos kryptį?

Jei plokštumoje yra dvi viena kitai statmenos kryptys, kurių vienoje jungtis neleidžia kūnui judėti, o kitoje ne, tai jo reakcijos kryptis yra priešinga pirmajai krypčiai.

Apskritai ryšio reakcija nukreipta priešinga kryptimi nei ta, kuria jungtis neleidžia kūnui judėti.

	Fiksuotas vyris Mobilusis

3. Jėgos momentas apie centrą

Galios akimirka F kurio nors fiksuoto centro atžvilgiu O yra vektorius, esantis statmenai plokštumai, einančia per jėgos vektorių, o centras O nukreiptas ta kryptimi, kad žiūrint iš jo galo būtų matyti jėgos sukimasis F centro O atžvilgiu prieš laikrodžio rodyklę.

Jėgos momento, palyginti su centru, savybės:

	1) Jėgos momento modulis centro atžvilgiu gali būti išreikštas dvigubu trikampio plotu OAV (1.1) 2) Jėgos momentas centro atžvilgiu lygus nuliui tuo atveju, kai jėgos veikimo linija eina per šį tašką, tai yra h = 0 .
	3) Jei iš taško APIE iki jėgos taikymo taško A nubrėžkite spindulio vektorių, tada jėgos momento vektorius gali būti išreikštas vektorine sandauga (1.2)
	4) Kai jėga perkeliama išilgai jos veikimo linijos, jos momento vektorius tam tikro taško atžvilgiu nekinta.

Jei kietam kūnui taikomos kelios toje pačioje plokštumoje esančios jėgos, galite apskaičiuoti algebrinę šių jėgų momentų sumą bet kurio šios plokštumos taško atžvilgiu.

Momentas M O , lygus tam tikros sistemos momentų algebrinei sumai bet kurio tos pačios plokštumos taško atžvilgiu, vadinamas pagrindinis jėgų sistemos momentas palyginti su šiuo tašku.

3. Jėgos momentas apie ašį

Norėdami nustatyti jėgos momentą apie ašį, turite:

1) nubrėžti plokštumą, statmeną Z ašiai;

2) nustatyti tašką APIE ašies susikirtimas su plokštuma;

3) projektuoja jėgą statmenai Fį šią plokštumą;

4) rasti jėgos projekcijos momentą F ašies susikirtimo su plokštuma taško O atžvilgiu.

Pasirašymo taisyklė:

Jėgos momentas ašies atžvilgiu laikomas teigiamu, jei žiūrint į Z ašį , galima pamatyti projekciją, linkusią pasukti plokštumą aš aplink Z ašį priešinga sukimuisi pagal laikrodžio rodyklę kryptimi.

Jėgos momento savybės ašies atžvilgiu 1) Jėgos momentas ašies atžvilgiu pavaizduotas atkarpa, nubrėžta išilgai Z ašies nuo taško O teigiama kryptimi, jei > 0 ir neigiama, jei< 0. 2) Jėgos momento apie ašį reikšmė gali būti išreikšta dvigubu plotu Δ (1.5) 3) Jėgos momentas ašies atžvilgiu yra lygus nuliui dviem atvejais: Jeigu F 1 = 0, tai yra, jėgos veikimo linija lygiagreti ašiai; jeigu h 1 = 0 , tai yra, jėgos veikimo linija kerta ašį.

4. Pora jėgų. Jėgų poros vektorius ir algebrinis momentas

Dviejų dydžių lygiagrečių ir priešingai nukreiptų jėgų sistema ir vadinama pora jėgų.

Plokštuma, kurioje yra jėgų ir veikimo linijos, vadinama jėgų poros veikimo plokštuma.

Trumpiausias atstumas h tarp porą sudarančių jėgų veikimo linijų vadinamas poros jėgų petys.

Poros jėgų akimirka nustatomas vienos iš poros ir peties jėgų modulio sandauga.

Ženklų taisyklė

Poros momento vektorius M nukreiptas statmenai jėgų poros veikimo plokštumai tokia kryptimi, kad, žiūrint į šį vektorių, matytųsi jėgų pora, linkusi sukti savo veikimo plokštumą priešinga kryptimi. iki sukimosi pagal laikrodžio rodyklę.

1. 4. Jėgų porų savybės plokštumoje

1 nuosavybė. Momento vektorius M poros pagal dydį ir kryptį yra lygios vektoriaus spindulio vektorinei sandaugai ABį šios poros jėgų, į kurios pradžią nukreiptas spindulio vektorius, jėgų AB, tai yra

(1.7)

2 nuosavybė. Pagrindinis jėgų, sudarančių porą, momentas, palyginti su savavališku tašku poros veikimo plokštumoje, nepriklauso nuo šio taško padėties ir yra lygus šios jėgų poros momentui.

5. Jėgų porų lygiavertiškumo sąlygos

Teorema apie jėgų porų lygiavertiškumo sąlygą,

guli toje pačioje plokštumoje.

Su pora jėgų yra dviejų vienodo dydžio, lygiagrečių ir skirtingomis kryptimis nukreiptų jėgų sistema.

Panagrinėkime jėgų sistemą (R; B"), sudarant porą.

Pora jėgų sukelia kūno sukimąsi ir jos poveikis kūnui matuojamas momentu. Jėgos, patenkančios į porą, nėra subalansuotos, nes jos taikomos dviem taškams (4.1 pav.).

Jų poveikio kūnui negalima pakeisti viena jėga (rezultatu).

Jėgų poros momentas skaitine prasme lygus jėgos modulio sandaugai ir atstumo tarp jėgų veikimo linijų (poros petys).

Momentas laikomas teigiamu, jei pora sukasi kūną pagal laikrodžio rodyklę (4.1 pav. (b)):

M(F;F") = Fa; M > 0.

Plokštuma, einanti per poros jėgų veikimo linijas, vadinama poros veikimo plokštuma.

Porų savybės(be įrodymų):

1. Jėgų pora gali būti judama jos veikimo plokštumoje.

2. Porų lygiavertiškumas.

Dvi poros, kurių momentai lygūs (4.2 pav.), yra lygiavertės (jų poveikis organizmui panašus).

3. Jėgų porų sudėjimas. Jėgų porų sistema gali būti pakeista gaunama pora.

Gaunamosios poros momentas lygus porų, sudarančių sistemą, momentų algebrinei sumai (4.3 pav.):

4. Porų pusiausvyra.

Porų pusiausvyrai būtina ir pakanka, kad sistemos porų momentų algebrinė suma būtų lygi nuliui:

Darbo pabaiga -

Ši tema priklauso skyriui:

Teorinė mechanika

Teorinė mechanika.. paskaita.. tema: pagrindinės statikos sąvokos ir aksiomos..

Jei jums reikia papildomos medžiagos šia tema arba neradote to, ko ieškojote, rekomenduojame pasinaudoti paieška mūsų darbų duomenų bazėje:

Ką darysime su gauta medžiaga:

Jei ši medžiaga jums buvo naudinga, galite ją išsaugoti savo puslapyje socialiniuose tinkluose:

Tviteryje

Visos temos šiame skyriuje:

Teorinės mechanikos problemos
Teorinė mechanika yra mokslas apie mechaninį kietų kūnų judėjimą ir jų sąveiką. Mechaninis judėjimas suprantamas kaip kūno judėjimas erdvėje ir laike iš

Trečioji aksioma
Netrukdydami mechaninei kūno būsenai, galite pridėti arba pašalinti subalansuotą jėgų sistemą (principą atmesti jėgų sistemą, lygiavertę nuliui) (1.3 pav.). P, = P2 P, = P.

Antrosios ir trečiosios aksiomų pasekmė
Jėga, veikianti kietą kūną, gali būti judama išilgai jo veikimo linijos (1.6 pav.).

Ryšiai ir jungčių reakcijos
Visi statikos dėsniai ir teoremos galioja laisvam standžiam kūnui. Visi kūnai skirstomi į laisvuosius ir surištus. Laisvieji kūnai yra kūnai, kurių judėjimas nėra ribojamas.

Kietas strypas
Diagramose strypai pavaizduoti kaip stora ištisinė linija (1.9 pav.). Strypas gali

Fiksuotas vyris
Tvirtinimo taško negalima perkelti. Strypas gali laisvai suktis aplink vyrių ašį. Tokios atramos reakcija eina per vyrių ašį, bet

Plokštuminė konverguojančių jėgų sistema
Jėgų sistema, kurios veikimo linijos susikerta viename taške, vadinama konvergentine (2.1 pav.).

Susiliejančių jėgų rezultatas
Dviejų susikertančių jėgų rezultatas gali būti nustatytas naudojant lygiagretainį arba jėgų trikampį (4-oji aksioma) (žr. 2.2).

Plokščios konverguojančių jėgų sistemos pusiausvyros sąlyga
Kai jėgų sistema yra pusiausvyroje, rezultatas turi būti lygus nuliui, todėl geometrinėje konstrukcijoje paskutinio vektoriaus pabaiga turi sutapti su pirmojo vektoriaus pradžia. Jeigu

Pusiausvyros uždavinių sprendimas geometriniu metodu
Patogu naudoti geometrinį metodą, jei sistemoje yra trys jėgos. Spręsdami pusiausvyros uždavinius, laikykite kūną absoliučiai kietu (sukietėjusiu). Problemų sprendimo tvarka:

Sprendimas
1. Tvirtinimo strypuose atsirandančios jėgos yra lygios jėgoms, kuriomis strypai laiko apkrovą (5-oji statikos aksioma) (2.5a pav.). Nustatome galimas reakcijų kryptis dėl

Jėgos projekcija ašyje
Jėgos projekciją į ašį lemia ašies atkarpa, nupjauta statmenais, nuleistais į ašį nuo vektoriaus pradžios ir pabaigos (3.1 pav.).

Stiprumas analitiniu būdu
Rezultato dydis lygus jėgų sistemos vektorių (geometrinei) sumai. Gautą rezultatą nustatome geometriškai. Parinkime koordinačių sistemą, nustatykime visų užduočių projekcijas

Konverguojančios jėgos analitine forma
Remdamiesi tuo, kad rezultatas lygus nuliui, gauname: Sąlyga

Jėgos momentas apie tašką
Jėga, kuri nepereina per kūno prisitvirtinimo tašką, sukelia kūno sukimąsi taško atžvilgiu, todėl tokios jėgos poveikis kūnui vertinamas kaip momentas. Jėgos momentas rel.

Puanso teorema apie lygiagretų jėgų perdavimą
Jėga gali būti perkelta lygiagrečiai jos veikimo linijai; šiuo atveju reikia pridėti jėgų porą, kurios momentas yra lygus jėgos modulio ir atstumo, per kurį jėga perduodama, sandaugai.

Paskirstytos jėgos
Savavališkos jėgų sistemos veikimo linijos nesikerta viename taške, todėl, norint įvertinti kūno būklę, tokią sistemą reikėtų supaprastinti. Norėdami tai padaryti, visos sistemos jėgos savavališkai perkeliamos į vieną

Atskaitos taško įtaka
Atskaitos taškas pasirenkamas savavališkai. Pasikeitus atskaitos taško vietai, pagrindinio vektoriaus reikšmė nepasikeis. Pasikeis pagrindinio momento dydis perkeliant redukcijos tašką,

Plokščios jėgos sistema
1. Esant pusiausvyrai pagrindinis sistemos vektorius lygus nuliui. Analitinis pagrindinio vektoriaus nustatymas leidžia daryti išvadą:

Krovinių tipai
Pagal taikymo būdą apkrovos skirstomos į koncentruotas ir paskirstytas. Jei faktinis apkrovos perdavimas vyksta nežymiai mažame plote (tam tikrame taške), apkrova vadinama koncentruota

Jėgos momentas apie ašį
Jėgos momentas ašies atžvilgiu lygus jėgos projekcijos į ašiai statmeną plokštumą momentui ašies susikirtimo su plokštuma taško atžvilgiu (7.1 pav. a). MOO

Vektorius erdvėje
Erdvėje jėgos vektorius projektuojamas į tris tarpusavyje statmenas koordinačių ašis. Vektoriaus projekcijos sudaro stačiakampio gretasienio briaunas, jėgos vektorius sutampa su įstriža (7.2 pav.

Erdvinė konvergentinė jėgų sistema
Erdvinė konvergencinė jėgų sistema – tai ne vienoje plokštumoje esančių jėgų sistema, kurios veikimo linijos susikerta viename taške. Erdvinės sistemos rezultatas

Savavališkos erdvinės jėgų sistemos atvedimas į centrą O
Pateikta erdvinė jėgų sistema (7.5a pav.). Atveskime jį į centrą O. Jėgos turi būti perkeltos lygiagrečiai ir susidaro jėgų porų sistema. Kiekvienos iš šių porų momentas yra lygus

Vienarūšių plokščių kūnų svorio centras
(plokščios figūros) Labai dažnai reikia nustatyti įvairių plokščių kūnų ir sudėtingos formos geometrinių plokščių figūrų svorio centrą. Plokščiams kūnams galime rašyti: V =

Plokštumos figūrų svorio centro koordinačių nustatymas
Pastaba. Simetriškos figūros svorio centras yra simetrijos ašyje. Strypo svorio centras yra aukščio viduryje. Paprastų geometrinių figūrų svorio centrų padėtis gali

Taško kinematika
Turėkite erdvės, laiko, trajektorijos, kelio, greičio ir pagreičio idėją. Žinokite, kaip nurodyti taško judėjimą (natūralų ir koordinatinį). Žinokite pavadinimus

Nuvažiuotas atstumas
Kelias matuojamas išilgai trajektorijos važiavimo kryptimi. Pavadinimas - S, matavimo vienetai - metrai. Taško judėjimo lygtis: lygtį apibrėžianti

Kelionės greitis
Vektorinis dydis, kuris šiuo metu apibūdina judėjimo trajektorija greitį ir kryptį, vadinamas greičiu. Greitis yra vektorius, nukreiptas bet kuriuo momentu į

Taško pagreitis
Vektorinis dydis, apibūdinantis greičio pokyčio dydį ir kryptį, vadinamas taško pagreičiu. Taško greitis judant iš taško M1

Vienodas judėjimas
Tolygus judėjimas – tai judėjimas pastoviu greičiu: v = const. Tiesiai vienodam judėjimui (10.1 pav. a)

Vienodai kintamieji judesiai
Lygiai taip pat kintamas judėjimas yra judėjimas su pastoviu tangentiniu pagreičiu: at = const. Skirtas vienodam tiesiam judėjimui

Judėjimas į priekį
Transliacinis yra standaus kūno judėjimas, kai bet kuri tiesi linija ant kūno judant išlieka lygiagreti pradinei jo padėties (11.1, 11.2 pav.). At

Sukamasis judėjimas
Sukamojo judesio metu visi kūno taškai apibūdina apskritimus aplink bendrą fiksuotą ašį. Fiksuota ašis, aplink kurią sukasi visi kūno taškai, vadinama sukimosi ašimi.

Ypatingi sukimosi judesių atvejai
Tolygus sukimasis (kampinis greitis pastovus): ω =const Tolygaus sukimosi lygtis (dėsnis) šiuo atveju yra tokia:

Besisukančio kūno taškų greičiai ir pagreičiai
Kūnas sukasi aplink tašką O. Nustatykime taško A, esančio atstumu RA nuo sukimosi ašies, judėjimo parametrus (11.6, 11.7 pav.). Kelias

Sprendimas
1. 1 sekcija – netolygus pagreitintas judėjimas, ω = φ’; ε = ω’ 2. 2 sekcija - greitis pastovus - judėjimas tolygus, . ω = const 3.

Pagrindiniai apibrėžimai
Sudėtingas judesys – tai judesys, kurį galima suskirstyti į kelis paprastus. Paprasti judesiai laikomi transliaciniais ir sukamaisiais. Apsvarstykite sudėtingą taškų judėjimą

Plokštuminis lygiagretus standaus kūno judėjimas
Plokščiasis lygiagretus arba plokščias standaus kūno judėjimas vadinamas tokiu, kad visi kūno taškai juda lygiagrečiai tam tikram fiksuotam nagrinėjamoje atskaitos sistemoje.

Transliacinis ir rotacinis
Plokštuminis lygiagretus judėjimas skaidomas į du judesius: transliacinį su tam tikru poliumi ir sukamąjį šio poliaus atžvilgiu. Dekompozicija naudojamas nustatyti

Greičio centras
Bet kurio kūno taško greitį galima nustatyti naudojant momentinį greičių centrą. Šiuo atveju sudėtingas judėjimas vaizduojamas sukimosi grandinės forma aplink skirtingus centrus. Užduotis

Dinamikos aksiomos
Dinamikos dėsniai apibendrina daugybės eksperimentų ir stebėjimų rezultatus. Dinamikos dėsnius, kurie paprastai laikomi aksiomomis, suformulavo Niutonas, tačiau taip pat buvo pirmasis ir ketvirtasis dėsniai.

Trinties samprata. Trinties rūšys
Trintis yra pasipriešinimas, kuris atsiranda, kai vienas šiurkštus kūnas juda kito paviršiumi. Kūnams slystant atsiranda slydimo trintis, o jiems riedant – riedėjimo trintis. Gamtos parama

Riedėjimo trintis
Pasipriešinimas riedėjimui yra susijęs su abipuse grunto ir rato deformacija ir yra žymiai mažesnis nei slydimo trintis. Paprastai dirvožemis laikomas minkštesniu nei ratas, tada dirvožemis daugiausia deformuojamas ir

Nemokami ir nemokami taškai
Materialus taškas, kurio judėjimas erdvėje nėra ribojamas jokiais ryšiais, vadinamas laisvuoju. Uždaviniai sprendžiami naudojant pagrindinį dinamikos dėsnį. Tada medžiaga

Inercijos jėga
Inercija yra gebėjimas išlaikyti savo būseną nepakitusią; tai yra vidinė visų materialių kūnų savybė. Inercijos jėga – tai jėga, atsirandanti greitėjant arba stabdant kūnus

Sprendimas
Aktyvios jėgos: varomoji jėga, trinties jėga, gravitacija. Reakcija atramoje R. Inercinę jėgą taikome priešinga nuo pagreičio kryptimi. Pagal d'Alemberto principą platformoje veikiančių jėgų sistema

Darbas atliekamas rezultatine jėga
Veikiant jėgų sistemai, taškas, kurio masė m, juda iš padėties M1 į padėtį M 2 (15.7 pav.). Judant veikiant jėgų sistemai, naudokite

Galia
Darbo našumui ir greičiui apibūdinti buvo įvesta galios sąvoka. Galia – darbas, atliktas per laiko vienetą:

Sukimosi galia
Ryžiai. 16.2 Kūnas juda spindulio lanku nuo taško M1 iki taško M2 M1M2 = φr Jėgos darbas

Efektyvumas
Kiekviena mašina ir mechanizmas, dirbdamas darbą, dalį energijos išeikvoja žalingiems pasipriešinimams įveikti. Taigi mašina (mechanizmas), be naudingo darbo, atlieka ir papildomus darbus.

Impulso kitimo teorema
Materialaus taško impulsas yra vektorinis dydis, lygus taško masės ir jo greičio mv sandaugai. Impulso vektorius sutampa su

Kinetinės energijos kitimo teorema
Energija – tai kūno gebėjimas atlikti mechaninį darbą. Yra dvi mechaninės energijos formos: potenciali energija arba padėties energija ir kinetinė energija.

Materialių taškų sistemos dinamikos pagrindai
Sąveikos jėgomis sujungtų materialių taškų rinkinys vadinamas mechanine sistema. Bet koks materialus kūnas mechanikoje laikomas mechaniniu

Pagrindinė besisukančio kūno dinamikos lygtis
Tegul standus kūnas, veikiamas išorinių jėgų, sukasi aplink Ozo ašį kampiniu greičiu

Įtampos
Pjūvio metodas leidžia nustatyti vidinės jėgos koeficiento reikšmę ruože, bet neleidžia nustatyti vidinių jėgų pasiskirstymo per atkarpą dėsnio. Norint įvertinti n stiprumą

Vidinės jėgos veiksniai, įtampos. Diagramų konstravimas
Turėkite idėją apie išilgines jėgas ir normalius įtempius skerspjūviuose. Žinoti išilginių jėgų ir normaliųjų įtempių diagramų sudarymo taisykles, pasiskirstymo dėsnį

Išilginės jėgos
Panagrinėkime siją, apkrautą išorinėmis jėgomis išilgai savo ašies. Sija tvirtinama sienoje (tvirtinimo „fiksavimas“) (20.2a pav.). Siją padalijame į pakrovimo zonas. Pakrovimo zona su

Plokščiųjų pjūvių geometrinės charakteristikos
Turėti supratimą apie ašinių, išcentrinių ir polinių inercijos momentų, pagrindinių centrinių ašių ir pagrindinių centrinių inercijos momentų nustatymo fizinę prasmę ir procedūrą.

Statinis pjūvio ploto momentas
Panagrinėkime savavališką atkarpą (25.1 pav.). Jei atkarpą padalinsime į be galo mažus plotus dA ir kiekvieną plotą padauginsime iš atstumo iki koordinačių ašies ir gautą

Išcentrinis inercijos momentas
Atkarpos išcentrinis inercijos momentas yra elementariųjų plotų sandaugų suma, perimta abi koordinatės:

Ašiniai inercijos momentai
Pjūvio ašinis inercijos momentas tam tikro kiemo, esančio toje pačioje plokštumoje, atžvilgiu vadinamas elementarių plotų sandaugų suma, perimta per visą plotą jų atstumo kvadratu.

Pjūvio poliarinis inercijos momentas
Pjūvio polinis inercijos momentas tam tikro taško (poliaus) atžvilgiu yra elementariųjų plotų sandaugų suma, perimta per visą plotą iš jų atstumo iki šio taško kvadratu:

Paprasčiausių atkarpų inercijos momentai
Stačiakampio ašiniai inercijos momentai (25.2 pav.) Įsivaizduokite tiesiogiai

Apskritimo poliarinis inercijos momentas
Apskritimui pirmiausia apskaičiuokite polinį inercijos momentą, tada ašinį. Įsivaizduokime apskritimą kaip be galo plonų žiedų rinkinį (25.3 pav.).

Torsioninė deformacija
Apvalios sijos sukimasis atsiranda tada, kai ji apkraunama jėgų poromis, kurių momentai yra statmenos išilginei ašiai plokštumose. Šiuo atveju sijos generatricos yra sulenktos ir pasuktos kampu γ,

Sukimo hipotezės
1. Išsipildžiusi plokščių pjūvių hipotezė: sijos skerspjūvis plokščias ir statmenas išilginei ašiai po deformacijos lieka plokščias ir statmenas išilginei ašiai.

Vidinės jėgos veiksniai sukimo metu
Sukimas – tai apkrova, kai sijos skerspjūvyje atsiranda tik vienas vidinės jėgos faktorius – sukimo momentas. Išorinės apkrovos taip pat yra dvi

Sukimo momento diagramos
Sukimo momentai gali skirtis išilgai sijos ašies. Nustatę momentų reikšmes išilgai sekcijų, sudarome sukimo momentų grafiką išilgai sijos ašies.

Torsioninis stresas
Sijos paviršiuje nubrėžiame išilginių ir skersinių linijų tinklelį ir atsižvelgiame į paviršiuje susidariusį raštą po Fig. 27.1a deformacija (27.1a pav.). Pop

Didžiausi sukimo įtempiai
Iš įtempių nustatymo formulės ir tangentinių įtempių pasiskirstymo sukimo metu diagramos aišku, kad didžiausi įtempimai atsiranda paviršiuje. Nustatykime maksimalią įtampą

Stiprumo skaičiavimo tipai
Yra dviejų tipų stiprumo skaičiavimai: 1. Projektinis skaičiavimas – nustatomas sijos (veleno) skersmuo pavojingoje atkarpoje:

Standumo skaičiavimas
Skaičiuojant standumą, nustatoma deformacija ir lyginama su leistina. Panagrinėkime apvalios sijos deformaciją veikiant išorinei jėgų porai, kurios momentas t (27.4 pav.).

Pagrindiniai apibrėžimai
Lenkimas yra apkrovos rūšis, kai sijos skerspjūvyje atsiranda vidinės jėgos faktorius – lenkimo momentas. Apdirbama mediena

Vidinės jėgos veiksniai lenkimo metu
Pavyzdys 1. Apsvarstykite spindulį, kurį veikia jėgų pora, kurios momentas m ir išorinė jėga F (29.3a pav.). Vidinės jėgos veiksniams nustatyti naudojame metodą su

Lenkimo akimirkos
Skersinė jėga atkarpoje laikoma teigiama, jei ji linkusi ją pasukti

Diferencialinės priklausomybės tiesioginiam skersiniam lenkimui
Šlyties jėgų ir lenkimo momentų diagramų sudarymas labai supaprastinamas naudojant skirtingą ryšį tarp lenkimo momento, šlyties jėgos ir vienodo intensyvumo

Sekcijos metodo naudojimas Gautą išraišką galima apibendrinti
Skersinė jėga nagrinėjamame ruože yra lygi visų jėgų, veikiančių siją iki nagrinėjamos atkarpos, algebrinei sumai: Q = ΣFi Kadangi kalbame

Įtampos
Panagrinėkime sijos, suspaustos į dešinę ir apkrautos sutelkta jėga F, lenkimą (33.1 pav.).

Streso būsena tam tikru momentu
Įtempta būsena taške pasižymi normaliais ir tangentiniais įtempiais, atsirandančiais visose per šį tašką einančiose srityse (atkarpose). Dažniausiai užtenka nustatyti pvz

Sudėtingos deformuotos būsenos samprata
Deformacijų, vykstančių skirtingomis kryptimis ir skirtingose ​​plokštumose, einančių per tašką, rinkinys lemia deformacijos būseną šiame taške. Sudėtinga deformacija

Apvalios sijos lenkimui su sukimu skaičiavimas
Skaičiuojant apvalią siją, veikiant lenkimui ir sukimui (34.3 pav.), būtina atsižvelgti į normalius ir tangentinius įtempius, nes abiem atvejais susidaro didžiausios įtempių vertės.

Stabilios ir nestabilios pusiausvyros samprata
Santykinai trumpi ir masyvūs strypai yra skirti suspaudimui, nes jie sugenda dėl sunaikinimo arba liekamųjų deformacijų. Mažo skerspjūvio ilgi strypai, skirti darbui

Stabilumo skaičiavimas
Stabilumo skaičiavimas susideda iš leistinos gniuždymo jėgos ir, palyginti su ja, veikiančios jėgos:

Skaičiavimas naudojant Eilerio formulę
Kritinės jėgos nustatymo uždavinį matematiškai išsprendė L. Euleris 1744. Strypui, šarnyriniam iš abiejų pusių (36.2 pav.), Eilerio formulė turi tokią formą.

Kritinės įtampos
Kritinis įtempis yra gniuždymo įtempis, atitinkantis kritinę jėgą. Suspaudimo jėgos įtempis nustatomas pagal formulę

Eilerio formulės taikymo ribos
Eilerio formulė galioja tik tampriųjų deformacijų ribose. Taigi kritinis įtempis turi būti mažesnis už medžiagos tamprumo ribą. Ankst