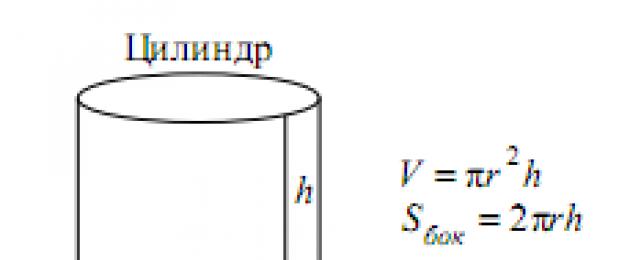Duotos dvi dėžės taisyklingos keturkampės prizmės. Taisyklinga keturkampė prizmė. Šios matematikos problemos grožis yra ne tik rezultato žinojimas, bet ir supratimas, kodėl strategija veikia

Bazinio lygio vieningo valstybinio egzamino 13 užduotyje nagrinėsime stereometrijos problemas, bet ne abstrakčias, o su iliustraciniais pavyzdžiais. Tai gali būti problemos dėl skysčio lygio induose, kurias aptariau toliau, arba problemos keičiant figūrą, pavyzdžiui, kurios viršūnės buvo nupjautos. Turite būti pasiruošę išspręsti paprastas stereometrijos problemas – jos dažniausiai kyla tiesiai į problemas plokštumoje, tereikia teisingai pažvelgti į piešinį.

Bazinio lygio matematikos vieningo valstybinio egzamino užduočių Nr.13 tipinių variantų analizė

Variantas 13MB1

Vanduo cilindriniame inde yra lygyje h = 80 cm. Kokiame lygyje bus vanduo, jei jis bus pilamas į kitą cilindrinį indą, kurio pagrindo spindulys yra 4 kartus didesnis už šį? Pateikite savo atsakymą centimetrais.

Vykdymo algoritmas:

1. Užrašykite cilindro tūrio formulę.
2. Pirmuoju ir antruoju atveju cilindro vertes pakeiskite skysčiu.
3. Išspręskite gautą antrojo aukščio h 2 lygtį.
4. Pakeiskite duomenis ir apskaičiuokite norimą vertę.

Sprendimas:

Užrašykime cilindro tūrio formulę.

Jei pamiršote cilindro tūrio formulę, leiskite jums priminti, kaip galite lengvai ją išvesti. Paprastų formų, tokių kaip kubeliai ir cilindrai, tūrį galima apskaičiuoti padauginus pagrindo plotą iš aukščio. Pagrindo plotas cilindro atveju yra lygus apskritimo plotui, kurį tikriausiai atsimenate: π r 2.

Todėl cilindro tūris lygus π r 2 h

Pirmuoju ir antruoju atveju cilindro vertes pakeiskime skysčiu.

V 1 = π r 1 2 h 1

V 2 = π r 2 2 h 2

Skysčio tūris nesikeitė, todėl tūrius galima sulyginti.

Kairės pusės yra lygios, o tai reiškia, kad dešinės pusės gali būti lygios.

π r 1 2 h 1 = π r 2 2 h 2

Išspręskime gautą lygtį antrojo aukščio h 2 atžvilgiu.

h 2 – nežinomas faktorius. Norėdami rasti nežinomą veiksnį, turite padalyti produktą iš žinomo faktoriaus.

h 2 =(π r 1 2 h 1)/ π r 2 2

Pagal sąlygą bazinis plotas tapo 4 kartus didesnis, tai yra, r 2 = 4 r 1.

Pakeiskime r 2 = 4 r 1 į h 1 išraišką.

Gauname: h 2 =(π r 1 2 h 1)/ π (4 r 1) 2

Gautą trupmeną sumažiname π, gauname h 2 = (r 1 2 h 1)/ 16 r 1 2

Gautą trupmeną sumažiname r 1, gauname h 2 = h 1 / 16.

Pakeiskime žinomus duomenis: h 2 = 80/ 16 = 5 cm.

13MB2 variantas

Duotos dvi taisyklingos keturkampės prizmės formos dėžės. Pirmasis langelis yra keturis su puse karto aukštesnis už antrąjį, o antrasis yra tris kartus platesnis nei pirmasis. Kiek kartų pirmosios dėžutės tūris yra mažesnis už antrosios?

Vykdymo algoritmas:

1. Raskite tūrio santykį.
2. Sumažinkite gautą frakciją.

Sprendimas:

V 1 = a 1 b 1 c 1

V 2 = a 2 b 2 c 2

Raskime tūrių santykį.

Pagal sąlygą c 1 = 4,5 c 2 (pirmasis langelis keturis su puse karto didesnis nei antrasis),

b 2 = 3 b 1 (antrasis langelis tris kartus platesnis nei pirmasis).

V 1 / V 2 = (a 1 b 1 c 1)/ (a 2 b 2 c 2) = (a 1 b 1 4,5 c 2)/ (3a 1 3b 1 c 2 ) = (a 1 b 1 4,5 c 2)/ (9a 1 b 1 c 2)

V 1 / V 2 = (a 1 b 1 4,5 c 2) / (9a 1 b 1 c 2) = 4,5/9 = ½.

Pirmosios dėžutės tūris yra 2 kartus mažesnis nei antrosios.

Variantas 13MB3

Duotos dvi taisyklingos keturkampės prizmės formos dėžės. Pirmasis langelis yra pusantro karto aukštesnis už antrąjį, o antrasis - tris kartus platesnis nei pirmasis. Kiek kartų pirmosios dėžutės tūris yra mažesnis už antrosios?

Vykdymo algoritmas:

1. Užrašykite taisyklingos keturkampės prizmės tūrio apskaičiavimo formulę.
2. Bendra forma užrašykite tūrio nustatymo formulę pirmuoju ir antruoju atveju.
3. Raskite tūrio santykį.
4. Transformuokite gautą išraišką atsižvelgdami į pirmosios ir antrosios prizmių išmatavimų santykį.
5. Sumažinkite gautą frakciją.

Sprendimas:

Užsirašykime formulę taisyklingosios keturkampės prizmės tūriui apskaičiuoti.

Bendrai užrašykime tūrio nustatymo formulę pirmuoju ir antruoju atveju.

V 1 = a 1 b 1 c 1

V 2 = a 2 b 2 c 2

Raskime tūrių santykį.

V 1 / V 2 = (a 1 b 1 c 1) / (a ​​2 b 2 c 2)

Transformuokime gautą išraišką atsižvelgdami į pirmosios ir antrosios prizmių išmatavimų santykį.

Pagal sąlygą c 1 = 1,5 c 2 (pirmasis langelis yra pusantro karto didesnis nei antrasis), b 2 = 3 b 1 (antrasis langelis tris kartus platesnis už pirmąjį).

Kadangi tai yra taisyklingos keturkampės prizmės, prie pagrindo yra kvadratas, o tai reiškia, kad antrojo langelio gylis taip pat tris kartus didesnis už pirmosios, tai yra, a 2 = 3 a 1

Pakeiskime šias išraiškas į tūrio santykio formulę:

V 1 / V 2 = (a 1 b 1 c 1)/ (a 2 b 2 c 2) = (a 1 b 1 1,5 c 2)/ (3a 1 3b 1 c 2 ) = (a 1 b 1 1,5 c 2)/ (9a 1 b 1 c 2)

Sumažinkime gautą trupmeną a 1 · b 1 · c 2 . Mes gauname:

V 1 / V 2 = (a 1 b 1 1,5 c 2)/ (9a 1 b 1 c 2) = 1,5/9 = 15/(10 9) = 3/(2 9 ) = 1/ (2 · 3) = 1/6.

Pirmosios dėžutės tūris yra 6 kartus mažesnis nei antrosios.

Atsakymas: 6.

Variantas 13MB4

Visos jo viršūnės buvo nupjautos iš medinio kubo (žr. pav.). Kiek veidų turi gautas daugiakampis (nematomos briaunos paveiksle nerodomos)?

Pirmiausia prisiminkime, kiek kubo veidų ir viršūnių turi: šešis veidus ir aštuonias viršūnes. Dabar kiekvienos viršūnės vietoje po pjovimo formuojamas naujas veidas, o tai reiškia, kad užduotyje modifikuotas kubas turi šešis originalius veidus ir aštuonis naujus (po pjovimo). Iš viso gauname: 6 + 8 = 14 veidų.

Jei mūsų paklaustų, kiek viršūnių turi naujasis „kubas“. Akivaizdu, kad jei vietoj vieno yra trys, o jų yra tik aštuoni, tada gauname: 8 3 = 24

Variantas 13MB5

Pateikiami du cilindrai. Pirmojo cilindro pagrindo spindulys ir aukštis yra atitinkamai 2 ir 6, o antrojo - 6 ir 4. Kiek kartų antrojo cilindro tūris yra didesnis už pirmojo?

Vykdymo algoritmas

1. Užrašome formulę cilindro tūriui apskaičiuoti.
2. Pateikiame pagrindo spindulio ir 1-ojo cilindro aukščio žymėjimą. Panašius 2-ojo cilindro parametrus išreiškiame panašiai.
3. Sudarome 1 ir 2 cilindrų tūrio formules.
4. Apskaičiuojame tūrio santykį.

Sprendimas:

Cilindro tūris yra: V=πR 2 H. 1-ojo cilindro pagrindo spindulį pažymėkime R 1, o aukštį – H 1. Atitinkamai, 2-ojo cilindro pagrindo spindulį žymime R 2, o aukštį - H 2.

Iš čia gauname: V 1 =πR 1 2 H1, V 2 =πR 2 2 H 2.

Užrašykime reikiamą tūrio santykį:

.

Į gautą ryšį pakeičiame skaitinius duomenis:

.

Išvada: 2-ojo cilindro tūris yra 6 kartus didesnis nei 1-ojo.

13MB6 variantas

5 litrai vandens supilami į tiesios prizmės formos baką. Kai dalis buvo visiškai panardinta į vandenį, vandens lygis bake pakilo 1,4 karto. Raskite dalies tūrį. Pateikite savo atsakymą kubiniais centimetrais, žinodami, kad viename litre yra 1000 kubinių centimetrų.

Vykdymo algoritmas

1. Pristatome tūrio žymėjimus prieš ir po detalės panardinimo. Tegul būna atitinkamai V 1 Ir V 2.
2. Mes nustatome vertę V 1. Mes išreiškiame V 2 per V 1. Vertės radimas V 2.
3. Gautą rezultatą litrais paverčiame kubiniais cm.

Sprendimas:

Bako tūris prieš nardymą V 1=5 (l). Nes panardinus detalę tūris tapo lygus V 2. Pagal būklę padidėjo 1,4 karto, taigi V 2=1,4V 1.

Iš čia gauname: V 2=1,4·5=7 (l).

Taigi tūrių skirtumas, sudarantis dalies tūrį, yra lygus:

V 2 – V 1=7–5=2 (l).

2 l=2·1000=2000 (cc).

Variantas 13MB7

Vanduo cilindriniame inde yra lygyje h = 80 cm. Kokiame lygyje bus vanduo, jei jis bus pilamas į kitą cilindrinį indą, kurio pagrindo spindulys yra du kartus didesnis už pirmojo? Pateikite savo atsakymą centimetrais.

Vykdymo algoritmas

1. Užrašome formulę cilindro tūriui apskaičiuoti.
2. Remdamiesi šia formule, užrašome 2 lygtis – vandens tūriui 1 ir 2 induose apskaičiuoti. Norėdami tai padaryti, formulėje naudojame atitinkamus indeksus 1 ir 2.
3. Kadangi vanduo tiesiog pilamas iš vieno indo į kitą, jo tūris nesikeičia. Todėl gautas lygtis sulyginame. Iš gautos vienos lygties randame vandens lygį 2-ajame inde, išreikštą aukščiu h 2.

Sprendimas:

Cilindro tūris yra: V=S bazė h=πR 2 val.

Vandens tūris 1 inde: V 1 =πR 1 2 h 1.

Tūris 2 inde: V 2 =πR 2 2 h 2.

Mes lygiuojamės V 1 Ir V 2: πR 1 2 h 1 = πR 2 2 h 2.

Sumažiname π ir išreiškiame h 2:

.

Pagal sąlygą R 2=2R 1. Iš čia:

Variantas 13MB8

Visos jo viršūnės buvo nupjautos iš medinės taisyklingos trikampės prizmės (žr. pav.). Kiek viršūnių turi gautas daugiakampis (nematomos briaunos paveikslėlyje nerodomos)?

Vykdymo algoritmas

1. Nustatykite trikampės prizmės viršūnių skaičių.
2. Išanalizuokime pokyčius, kurie įvyks pjaunant visas viršūnes. Suskaičiuojame naujojo daugiakampio viršūnių skaičių.

Sprendimas:

Prizmės viršūnės sudaro pagrindų (viršutinės ir apatinės) viršūnes. Kadangi taisyklingosios trikampės prizmės pagrindai yra taisyklingieji trikampiai, tai tokia prizmė turi 3·2=6 viršūnes.

Nupjovę prizmės viršūnes, vietoj jų gauname mažus (lyginant su pačios prizmės dydžiu) trikampius. Tai taip pat parodyta paveikslėlyje. Tai yra, vietoj kiekvienos viršūnės susidaro 3 naujos. Vadinasi, jų skaičius taps lygus: 6·3=18.

Variantas 13MB9

Pateiktos dvi taisyklingos keturkampės prizmės formos dėžės, stovinčios ant pagrindo. Pirmasis langelis yra keturis su puse karto žemesnis nei antrasis, o antrasis yra siauresnis nei pirmasis. Kiek kartų pirmosios dėžutės tūris yra didesnis už antrosios?

Vykdymo algoritmas

1. Pateikiame dėžių linijinių parametrų ir jų tūrių žymes.
2. Pagal sąlygą nustatome tiesinių parametrų priklausomybę.
3. Užrašome prizmės tūrio skaičiavimo formulę.
4. Šią formulę pritaikykime dėžių tūriui.
5. Tūrių santykio radimas.

Sprendimas:

Nes Dėžių forma yra taisyklinga prizmė, tada jų pagrindai yra kvadratai. Todėl kiekvienos dėžutės ilgį ir plotį galime nurodyti vienodai. Tebūnie tai pirmai dėžutei a 1, ir antram a 2. Atitinkamai pažymime dėžių aukščius h 1 Ir h 2. Apimtys – V 1 Ir V 2.

Pagal būklę, h 2=4,5h 1, a 1=3a 2.

Prizmės tūris lygus: V=S pagrindinis h. Nes tada dėžių apačioje yra kvadratas S pagrindinis =a 2. Iš čia: V=a 2 val.

1-ajai dėžutei turime: V 1 =a 1 2 h 1. 2-ajam langeliui: V 2 =a 2 2 h 2.

Tada gauname santykį:

Variantas 13MB10

Kūgio formos inde skysčio lygis pasiekia ½ aukščio. Indo tūris 1600 ml. Koks išpilamo skysčio tūris? Atsakymą pateikite mililitrais.

Vykdymo algoritmas

1. Įrodome, kad sąlygoje pateikti kūgiai yra panašūs.
2. Nustatome panašumo koeficientą.
3. Naudodamiesi panašių kūnų tūrių savybe, randame skysčio tūrį.

Sprendimas:

Jei apsvarstysime kūgio pjūvį išilgai dviejų priešingų jo generatricų (ašinė pjūvis), pamatysime, kad tokiu būdu gauti didelio ir mažojo kūgio (sudaro skysčio) trikampiai yra panašūs. Tai išplaukia iš jų kampų lygybės. Tie. turime: kūgių aukščiai ir pagrindo spinduliai panašūs. Iš to darome išvadą: nes Jei kūgių linijiniai parametrai yra panašūs, tada kūgiai yra panašūs.

Pagal būklę mažo kūgio (skysčio) aukštis yra ½ kūgio aukščio. Tai reiškia, kad mažų ir didelių kūgių panašumo koeficientas yra ½.

Taikome kūnų panašumą, kuris susideda iš to, kad jų tūriai yra susiję kaip panašumo koeficientas kube. Pažymime didelio kūgio tūrį V 1, mažas - V 2. Mes gauname:

.

Kadangi pagal sąlygą V 1= 1600 ml, tada V 2=1600/8=200 ml.

Variantas 13MB11

Duoti du rutuliai, kurių spindulys yra 4 ir 1. Kiek kartų didesnio rutulio tūris didesnis už mažesnio?

Vykdymo algoritmas

1. Užrašome rutulio tūrio skaičiavimo formulę.
2. Kiekvienam rutuliui pritaikykime formulę. Norėdami tai padaryti, naudojame indeksus 1 ir 2.
3. Užrašome tūrio santykį ir jį apskaičiuojame pakeisdami skaitinius duomenis iš sąlygos.

Sprendimas:

Rutulio tūris apskaičiuojamas pagal formulę: .

Taigi 1-ojo (didesnio) rutulio tūris yra lygus , 2-as (mažesnis) rutulys – .

Sukurkime tūrių santykį:

Sąlygos skaitinius duomenis pakeičiame į gautą formulę:

Išvada: didesnio rutulio tūris yra 64 kartus didesnis.

Variantas 13MB12

Pateikiami du cilindrai. Pirmojo cilindro pagrindo spindulys ir aukštis yra atitinkamai 4 ir 18, o antrojo – 2 ir 3. Kiek kartų pirmojo cilindro šoninio paviršiaus plotas yra didesnis už antrojo šoninio paviršiaus plotą. ?

Vykdymo algoritmas

1. Užrašome formulę, kad nustatytų cilindro šoninio paviršiaus plotą.
2. Perrašome du kartus naudodami atitinkamus indeksus - 1-am (didesniam) ir 2-am (mažesniam) cilindrui.
3. Rasti ploto santykį. Santykius apskaičiuojame naudodami skaitinius duomenis iš sąlygos.

Sprendimas:

Cilindro šoninio paviršiaus plotas apskaičiuojamas taip: S=2πRH.

1-ajam cilindrui turime: S1 =2π R 1 H 1. 2 cilindrui: S2 =2π R2H2.

Sukurkime šių sričių santykį:

Raskime gauto santykio skaitinę reikšmę:

Išvada: 1-ojo cilindro šoninio paviršiaus plotas yra 12 kartų didesnis.

Variantas 13MB13

Vienalytis 3 cm skersmens rutulys sveria 162 gramus. Kiek gramų sveria 2 cm skersmens rutulys, pagamintas iš tos pačios medžiagos?

Vykdymo algoritmas

1. Užrašome formulę didesnių rutuliukų masei pagal tankį ir tūrį nustatyti.
2. Šioje formulėje tūris rašomas per rutulio tūrį (per jo spindulį).
3. Užrašome mažesnio rutulio masės formulę, o tūrį – spindulį (pagal analogiją su 1 ir 2 pastraipomis).
4. Kadangi abu rutuliai pagaminti iš tos pačios medžiagos, rastą tankio reikšmę galime naudoti mažesnio rutulio masės formulėje. Apskaičiuojame reikiamą masę.

Sprendimas:

Didesnio (1-ojo) rutulio masė yra lygi: m 1 =ρ V 1. Šio rutulio tūris yra V 1 = Skystis pilamas į rezervuarą, suformuotą kaip taisyklinga keturkampė prizmė, kurios pagrindo kraštinė lygi 40 cm. Norint išmatuoti kompleksinės formos dalies tūrį, ji visiškai panardinama į šį skystį. Raskite detalės tūrį, jei ją panardinus skysčio lygis bake pakyla 10 cm. Pateikite atsakymą kubiniais centimetrais.

Vykdymo algoritmas

1. Nustatome prizmės dalį, atitinkančią panardintos dalies tūrį.
2. Dalies tūrį apskaičiuojame pagal formulę, skirtą tiesios prizmės su kvadratu prie pagrindo tūrio nustatymo formule.

Sprendimas:

Dalis, panardinta į skystį, užima tūrį, atitinkantį skysčio stulpelį, kurio aukštis yra 10 cm, t.y. skirtumas, atsirandantis tarp pradinio skysčio aukščio ir galutinio (po panardinimo). Tai reiškia, kad dalies tūris yra lygus skysčio daliai, užimančiai 40x40x10 (cm) tūrį.

Raskime šį tomą.

Kurį radau DataGenetics svetainėje. Su šiuo straipsniu susijusias klaidas prašome siųsti asmenine žinute.

Pagal šią problemą kalėjime yra 100 kalinių, kiekvienas jų sunumeruotas nuo 1 iki 100. Kalėjimo prižiūrėtojas nusprendžia suteikti kaliniams galimybę išeiti į laisvę, pasako jiems testo sąlygas ir jei visi kaliniai išlaikys testą, tada jie bus išleisti. Jei nors vienas iš jų neišlaikys testo, visi kaliniai mirs.

Užduotis

Kalėjimo prižiūrėtojas nueina į slaptą kambarį ir paruošia 100 dėžių su dangčiais. Ant kiekvienos dėžutės jis uždeda skaičius, sunumeruotus nuo 1 iki 100. Tada atneša 100 popierinių tablečių pagal kalinių skaičių ir šias lenteles sunumeruoja nuo 1 iki 100. Po to jis sumaišo 100 tablečių ir įdeda po vieną tabletę į kiekvieną dėžutę. uždarant dangtį. Kaliniai nemato, kaip kalėjimo prižiūrėtojas atlieka visus šiuos veiksmus.

Prasideda varžybos, kalėjimo prižiūrėtojas nuveda kiekvieną kalinį po vieną į kambarį su dėžėmis ir sako kaliniams, kad jie turi surasti dėžutę, kurioje bus lentelė su kalinio numeriu. Kaliniai bando rasti savo numerį atidarydami dėžes. Kiekvienam asmeniui leidžiama atidaryti iki 50 dėžių; jei kiekvienas iš kalinių ras savo numerį, tada kaliniai bus paleisti, jei bent vienas iš jų neras savo numerio per 50 bandymų, tada visi kaliniai mirs.

Kad kaliniai būtų paleisti, VISI kaliniai turi išlaikyti testą.

Taigi kokia tikimybė, kad kaliniai bus atleisti?

• Kaliniui atidarius dėžutę ir patikrinus ženklą, ji įdedama atgal į dėžę ir vėl uždaromas dangtis;
• Plokštės vietomis nekeičiamos;
• Prasidėjus testui, kaliniai negali vienas kitam palikti įkalčių arba kaip nors bendrauti tarpusavyje;
• Prieš pradedant testą, kaliniams leidžiama aptarti strategiją.

Kokia yra geriausia kalinių strategija?

Papildomas klausimas:

Jei kalinys (ne testo dalyvis) turės galimybę patekti į slaptą kambarį prieš bandymo pradžią, apžiūrėkite visus ženklus visuose langeliuose ir (nebūtina, bet nebūtina) sukeiskite du ženklus iš dviejų langelių ( tokiu atveju draugas neturės galimybės - informuoti kalinius apie savo veiksmų rezultatą), kokios strategijos jis turėtų imtis, kad padidintų kalinių galimybes išsigelbėti?

Ar sprendimas mažai tikėtinas?

Iš pirmo žvilgsnio ši užduotis atrodo beveik beviltiška. Panašu, kad galimybė kiekvienam kaliniui rasti savo planšetę yra mikroskopiškai maža. Be to, kaliniai negali keistis informacija vieni su kitais testo metu.

Vieno kalinio tikimybė yra 50:50. Yra tik 100 dėžių ir jis gali atidaryti iki 50 dėžių ieškodamas savo ženklo. Jei jis atidaro dėžutes atsitiktinai ir atidaro pusę visų dėžių, jis ras savo ženklą atviroje dėžių pusėje arba jo ženklas liks uždarytose 50 dėžių. Jo sėkmės tikimybė yra ½.

Paimkime du kalinius. Jei abu langelius pasirenka atsitiktinai, kiekvieno iš jų tikimybė bus ½, o abiejų - ½x½=¼.
(dviem kaliniams sėkmė bus vienu atveju iš keturių).

Trims kaliniams tikimybė bus ½ × ½ × ½ = ⅛.

100 kalinių tikimybė yra tokia: ½ × ½ × … ½ × ½ (padauginta iš 100 kartų).

Tai lygu

Pr ≈ 0,00000000000000000000000000000008

Tai yra, tai yra labai maža galimybė. Šioje situacijoje greičiausiai visi kaliniai bus mirę.

Neįtikėtinas atsakymas

Jei kiekvienas kalinys atsitiktinai atidarytų dėžes, vargu ar išlaikytų testą. Yra strategija, pagal kurią kaliniai gali tikėtis sėkmės daugiau nei 30 % laiko. Tai stulbinančiai neįtikėtinas rezultatas (jei anksčiau negirdėjote apie šią matematikos problemą).

Daugiau nei 30% visiems 100 kalinių! Taip, tai net geriau nei dviejų kalinių tikimybė, jei jie dėžes atidarys atsitiktinai. Bet kaip tai įmanoma?

Aišku, kad kiekvienam kaliniui po vieną, šansai negali būti didesni nei 50% (juk tarp kalinių nėra galimybės bendrauti). Tačiau nepamirškite, kad informacija saugoma plokščių išdėstyme dėžutėse. Niekas nemaišo ženklų tarp atskirų kalinių apsilankymų kambaryje, todėl galime pasinaudoti šia informacija.

Sprendimas

Pirmiausia papasakosiu jums sprendimą, tada paaiškinsiu, kodėl jis veikia.

Strategija yra labai paprasta. Pirmasis kalinys atidaro dėžutę su numeriu, užrašytu ant jo drabužių. Pavyzdžiui, kalinys numeris 78 atidaro dėžutę su numeriu 78. Jei jis ras savo numerį ant ženklo dėžutės viduje, puiku! Jei ne, jis žiūri į numerį ant plokštelės „savo“ langelyje ir atidaro kitą langelį su tuo numeriu. Atidaręs antrą dėžutę, jis žiūri į šios dėžutės viduje esančios plokštelės numerį ir atidaro trečią dėžutę su šiuo numeriu. Toliau šią strategiją tiesiog perkeliame į likusius langelius. Aiškumo dėlei žiūrėkite paveikslėlį:

Galų gale kalinys arba suras savo numerį, arba pasieks 50 dėžių ribą. Iš pirmo žvilgsnio tai atrodo beprasmiška, palyginti su tiesiog atsitiktiniu dėžutės parinkimu (ir vienam kaliniui tai daro), bet kadangi visi 100 kalinių naudos tą patį dėžių rinkinį, tai prasminga.

Šios matematikos problemos grožis yra ne tik rezultato žinojimas, bet ir supratimas Kodėlši strategija veikia.

Taigi kodėl strategija veikia?

Kiekvienoje dėžutėje yra vienas ženklas – ir šis ženklas yra unikalus. Tai reiškia, kad plokštelė yra dėžutėje su tuo pačiu numeriu arba ji nurodo kitą dėžutę. Kadangi visi ženklai yra unikalūs, kiekvienam langeliui yra tik vienas ženklas, rodantis į jį (ir tik vienas būdas patekti į tą langelį).

Jei pagalvoji, dėžutės sudaro uždarą apskritą grandinę. Vienas langelis gali būti tik vienos grandinės dalis, nes dėžutės viduje yra tik viena rodyklė į kitą ir atitinkamai ankstesniame langelyje yra tik viena žymeklis į tam tikrą langelį (programuotojai gali matyti analogiją su susietais sąrašais) .

Jei dėžutė nenurodo į save (dėžutės numeris lygus joje esančios plokštelės skaičiui), tada ji bus grandinėje. Kai kurios grandinės gali būti sudarytos iš dviejų dėžių, kai kurios yra ilgesnės.

Kadangi visi kaliniai pradeda nuo dėžės, kurios numeris yra toks pat kaip ir jų drabužių, jie pagal apibrėžimą yra dedami ant grandinės, kurioje yra jų ženklas (yra tik vienas ženklas, rodantis į tą dėžutę).

Tyrinėdami dėžutes ratu išilgai šios grandinės, jie garantuotai galiausiai suras savo ženklą.

Lieka tik klausimas, ar jie ras savo ženklą per 50 ėjimų.

Grandinės ilgis

Kad visi kaliniai išlaikytų testą, maksimalus grandinės ilgis turi būti mažesnis nei 50 dėžių. Jei grandinė yra ilgesnė nei 50 dėžių, kaliniai, turintys numerius iš šių grandinių, neišlaikys testo – ir visi kaliniai bus mirę.

Jei maksimalus ilgiausios grandinės ilgis yra mažesnis nei 50 dėžių, tada visi kaliniai išlaikys testą!

Pagalvokite apie tai sekundę. Pasirodo, bet kokiame plokščių išdėstyme gali būti tik viena grandinė ilgesnė nei 50 dėžių (turime tik 100 dėžių, todėl jei viena grandinė yra ilgesnė nei 50, tai likusi dalis bus trumpesnė nei 50) .

Ilgos grandinės sandorio tikimybė

Įsitikinus, kad norint pasisekti, maksimalus grandinės ilgis turi būti mažesnis arba lygus 50, o bet kuriame rinkinyje gali būti tik viena ilga grandinėlė, galime apskaičiuoti tikimybę, kad pavyks išlaikyti testą:

Dar šiek tiek matematikos

Taigi ko mums reikia norint išsiaiškinti ilgos grandinės egzistavimo tikimybę?

Jei grandinės ilgis l, tikimybė, kad dėžės bus už šios grandinės ribų, yra lygi:

Šioje skaičių rinkinyje yra (l-1)! ženklų išdėstymo būdai.

Likusius ženklus galima rasti (100-l)! būdai (nepamirškite, kad grandinės ilgis neviršija 50).

Atsižvelgiant į tai, permutacijų, turinčių tikslaus ilgio l grandinę, skaičius: (>50)

Pasirodo, yra 100(!) ženklų išdėstymo būdų, todėl l ilgio grandinės egzistavimo tikimybė lygi 1/l. Beje, šis rezultatas nepriklauso nuo dėžių skaičiaus.

Kaip jau žinome, gali būti tik vienas variantas, kurio ilgis > 50, todėl sėkmės tikimybė apskaičiuojama naudojant šią formulę:

Rezultatas

31,18% - tikimybė, kad ilgiausios grandinės dydis bus mažesnis nei 50 ir kiekvienas iš kalinių galės rasti savo ženklą, atsižvelgiant į 50 bandymų ribą.

Tikimybė, kad visi kaliniai ras savo ženklus ir išlaikys testą, yra 31,18%.

Žemiau yra grafikas, rodantis visų l ilgio grandinių (x ašyje) tikimybes (y ašyje). Raudona spalva žymi visus „gedimus“ (čia pateikta kreivė yra tik 1/l grafikas). Žalia reiškia "sėkmę" (šioje grafiko dalyje skaičiavimas yra šiek tiek sudėtingesnis, nes yra keli būdai nustatyti maksimalų ilgį<50). Общая вероятность складывается из зеленых столбцов в 31.18% шанс на спасение.

Harmoninis skaičius (ši straipsnio dalis skirta geeksams)

Matematikoje n-asis harmoninis skaičius yra pirmųjų n iš eilės skaičių natūraliosios eilutės atvirkštinių dydžių suma.

Apskaičiuokime limitą, jei vietoje 100a dėžučių turime savavališkai daug dėžučių (tarkime, kad iš viso turime 2n dėžučių).

Eulerio-Mascheroni konstanta yra konstanta, apibrėžiama kaip skirtumo tarp harmoninės serijos dalinės sumos ir skaičiaus natūralaus logaritmo riba.

Didėjant kalinių skaičiui, jei prižiūrėtojas leidžia kaliniams atidaryti pusę visų dėžių, išgelbėjimo tikimybė siekia 30,685%.

(Jei priėmėte sprendimą, pagal kurį kaliniai atsitiktinai atspėjo langelius, tada, didėjant kalinių skaičiui, išsigelbėjimo tikimybė yra lygi nuliui!)

Papildomas klausimas

Ar kas nors prisimena tolesnį klausimą? Ką mūsų naudingas draugas gali padaryti, kad padidintų mūsų galimybes išgyventi?

Dabar mes jau žinome sprendimą, todėl strategija čia paprasta: jis turi ištirti visus ženklus ir surasti ilgiausią dėžių grandinę. Jei ilgiausia grandinėlė yra mažesnė nei 50, tada plokštelių jam visai nereikia keisti arba keisti taip, kad ilgiausia grandinė netaptų ilgesnė nei 50. Tačiau jei jis randa ilgesnę nei 50 dėžučių grandinę, tereikia sukeisti dviejų dėžučių turinį iš tos grandinės, kad grandinė būtų padalinta į dvi trumpesnes grandines.

Dėl šios strategijos nebus ilgų grandinių ir visi kaliniai garantuotai ras savo ženklą ir išsigelbėjimą. Taigi, sukeisdami du ženklus, mes sumažiname išsigelbėjimo tikimybę iki 100%!

Darbo pobūdis: 8
Tema: Prizmė

Būklė

Įprastoje trikampėje prizmėje ABCA_1B_1C_1 pagrindo kraštinės yra 4, o šoninės briaunos yra 10. Raskite prizmės skerspjūvio plotą pagal plokštumą, einančią per kraštinių AB, AC, A_1B_1 ir A_1C_1 vidurio taškus.

Rodyti sprendimą

Sprendimas

Apsvarstykite toliau pateiktą paveikslą.

Todėl atkarpa MN yra trikampio A_1B_1C_1 vidurio linija MN = \frac12 B_1C_1=2. Taip pat, KL=\frac12BC=2. Be to, MK = NL = 10. Iš to seka, kad keturkampis MNLK yra lygiagretainis. Kadangi MK\parallel AA_1, tada MK\perp ABC ir MK\perp KL. Todėl keturkampis MNLK yra stačiakampis. S_(MNLK) = MK\cdot KL = 10\cdot 2 = 20.

Atsakymas

Darbo pobūdis: 8
Tema: Prizmė

Būklė

Taisyklingos keturkampės prizmės ABCDA_1B_1C_1D_1 tūris yra 24 . Taškas K yra briaunos CC_1 vidurys. Raskite piramidės KBCD tūrį.

Rodyti sprendimą

Sprendimas

Pagal sąlygą KC yra piramidės KBCD aukštis. CC_1 yra prizmės ABCDA_1B_1C_1D_1 aukštis.

Kadangi K yra CC_1 vidurio taškas, tada KC=\frac12CC_1. Tada tegul CC_1=H KC=\frac12H. Taip pat atkreipkite dėmesį į tai S_(BCD)=\frac12S_(ABCD). Tada V_(KBCD)= \frac13S_(BCD)\cdot\frac(H)(2)= \frac13\cdot\frac12S_(ABCD)\cdot\frac(H)(2)= \frac(1)(12)\cdot S_(ABCD)\cdot H= \frac(1)(12)V_(ABCDA_1B_1C_1D_1). Vadinasi, V_(KBCD)=\frac(1)(12)\cdot24=2.

Atsakymas

Šaltinis: „Matematika. Pasirengimas vieningam valstybiniam egzaminui 2017 m. Profilio lygis“. Red. F. F. Lysenko, S. Kulabukhova.

Darbo pobūdis: 8
Tema: Prizmė

Būklė

Raskite taisyklingos šešiakampės prizmės, kurios pagrindo kraštinė yra 6, o aukštis yra 8, šoninio paviršiaus plotą.

Rodyti sprendimą

Sprendimas

Prizmės šoninio paviršiaus plotas randamas pagal formulę S pusė. = P pagrindinis · h = 6a\cdot h, kur P bazinis. ir h yra atitinkamai pagrindo perimetras ir prizmės aukštis, lygus 8, o a yra taisyklingo šešiakampio kraštinė, lygi 6. Todėl S pusė. = 6\ctaškas 6\ctaškas 8 = 288.

Atsakymas

Šaltinis: „Matematika. Pasirengimas vieningam valstybiniam egzaminui 2017 m. Profilio lygis“. Red. F. F. Lysenko, S. Kulabukhova.

Darbo pobūdis: 8
Tema: Prizmė

Būklė

Vanduo buvo pilamas į taisyklingos trikampės prizmės formos indą. Vandens lygis siekia 40 cm Kokiame aukštyje bus vandens lygis, jei jis bus supiltas į kitą tokios pat formos indą, kurio pagrindo šonas yra dvigubai didesnis už pirmąjį? Išreikškite savo atsakymą centimetrais.

Rodyti sprendimą

Sprendimas

Tegu a yra pirmojo indo pagrindo kraštinė, tada 2 a yra antrojo indo pagrindo kraštinė. Pagal sąlygą skysčio V tūris pirmame ir antrame induose yra vienodas. Žymime H lygį, iki kurio pakilo skystis antrajame inde. Tada V= \frac12\cdot a^2\cdot\sin60^(\circ)\cdot40= \frac(a^2\sqrt3)(4)\cdot40, Ir, V=\frac((2a)^2\sqrt3)(4)\cdot H. Iš čia \frac(a^2\sqrt3)(4)\cdot40=\frac((2a)^2\sqrt3)(4)\cdot H, 40 = 4H, H = 10.

Atsakymas

Šaltinis: „Matematika. Pasirengimas vieningam valstybiniam egzaminui 2017 m. Profilio lygis“. Red. F. F. Lysenko, S. Kulabukhova.

Darbo pobūdis: 8
Tema: Prizmė

Būklė

Įprastoje šešiakampėje prizmėje ABCDEFA_1B_1C_1D_1E_1F_1 visos briaunos lygios 2. Raskite atstumą tarp taškų A ir E_1.

Rodyti sprendimą

Sprendimas

Trikampis AEE_1 yra stačiakampis, kadangi briauna EE_1 yra statmena prizmės pagrindo plokštumai, kampas AEE_1 bus stačiakampis.

Tada pagal Pitagoro teoremą AE_1^2 = AE^2 + EE_1^2. Raskime AE iš trikampio AFE naudodami kosinuso teoremą. Kiekvienas taisyklingo šešiakampio vidinis kampas yra 120^(\circ). Tada AE^2= AF^2+FE^2-2\cdot AF\cdot FE\cdot\cos120^(\circ)= 2^2+2^2-2\cdot2\cdot2\cdot\left (-\frac12 \right).

Taigi AE^2=4+4+4=12,

AE_1^2=12+4=16,

AE_1=4.

Atsakymas

Šaltinis: „Matematika. Pasirengimas vieningam valstybiniam egzaminui 2017 m. Profilio lygis“. Red. F. F. Lysenko, S. Kulabukhova.

Darbo pobūdis: 8
Tema: Prizmė

Būklė

Raskite tiesios prizmės, kurios pagrinde yra rombas, kurio įstrižainės yra lygios, šoninio paviršiaus plotą 4\sqrt5 ir 8, o šoninė briauna lygi 5.

Rodyti sprendimą

Sprendimas

Tiesios prizmės šoninio paviršiaus plotas randamas naudojant formulę S pusė. = P pagrindinis · h = 4a\cdot h, kur P bazinis. ir h atitinkamai pagrindo perimetras ir prizmės aukštis, lygus 5, o a yra rombo kraštinė. Raskime rombo kraštinę naudodamiesi tuo, kad rombo ABCD įstrižainės yra viena kitai statmenos ir perkirstos per pusę susikirtimo taško.

Pratimas:

Taisyklingoje keturkampėje prizmėje ABCDA 1 B 1 C 1 D 1 taškas K imamas kraštinėje CC 1 taip, kad SC: KS 1 = 1: 2.

a) Sukurkite prizmės pjūvį su plokštuma, einančia per taškus D ir K, lygiagrečią pagrindo AC įstrižai.

b) Raskite kampą tarp pjūvio plokštumos ir pagrindo plokštumos, jei CC 1 = 4,5√ 2, AB = 3.

Sprendimas:

a) Kadangi prizmė ABCDA 1 B 1 C 1 D 1 yra taisyklinga, tai ABCD yra kvadratas, o šoniniai paviršiai yra lygūs stačiakampiai.

Sukonstruokime prizmės pjūvį plokštuma, einančia per taškus D ir K lygiagrečiai AC. Pjovimo plokštumos ir plokštumos AA 1 C 1 susikirtimo linija eina per tašką K ir yra lygiagreti AC.

ACC 1 plokštumoje per tašką K nubrėžiame atkarpą KF lygiagrečiai įstrižai AC.

Kadangi prizmės paviršiai A 1 ADD 1 ir B 1 BCC 1 yra lygiagrečiai, tai pagal lygiagrečių plokštumų savybę pjūvio plokštumos ir šių paviršių susikirtimo linijos yra lygiagrečios. Darom PK || F.D. Keturkampis FPKD yra reikalinga sekcija.

b) Raskite kampą tarp pjūvio plokštumos ir pagrindo plokštumos. Tegul pjūvio plokštuma kerta pagrindinę plokštumą išilgai tiesės p, einančios per tašką D. AC || FK, todėl AC || p (jei plokštuma eina per tiesę, lygiagrečią kitai plokštumai ir kerta šią plokštumą, tai plokštumų susikirtimo linija yra lygiagreti šiai tiesei). Kadangi kvadrato įstrižainės yra viena kitai statmenos, tada BD ⊥ AC, o tai reiškia
BD ⊥ p. BD yra PD projekcija į plokštumą ABC, taigi PD ⊥ p pagal trijų statmenų teoremą. Todėl ∠PDB yra tiesinis dvikampis kampas tarp pjovimo plokštumos ir pagrindinės plokštumos.

FK || p, todėl FK ⊥ PD. Keturkampyje FPKD turime FD || PK ir KD || FP, o tai reiškia, kad FPKD yra lygiagretainis, o kadangi stačiakampiai trikampiai FAD ir KCD yra lygūs dviejose kojose (AD = DC kaip kvadrato kraštinės, FA = KC kaip atstumas tarp lygiagrečių tiesių AC ir F K), tada FPKD yra rombas. Taigi PD = 2OD.

Pagal CK sąlygą: KC 1 = 1: 2, tada KC = 1/3*CC 1 = 4,5√2 / 3 = 1,5√2.

V Δ DKC pagal Pitagoro teoremą KD 2 = DC 2 + KC 2 , KD = =
√13,5.

AC = 3√2 kaip kvadrato įstrižainė, OK = EC = 1/2*AC, OK = 1,5√2.

V Δ KOD pagal Pitagoro teoremą OD 2 = KD 2 − OK 2,

OD= = 3. PD = 2OD = 6.

Stačiakampiame trikampyje PBP cos ∠PDB = BD / PD = 3√2 / 6 = √2 / 2, todėl ∠PDB = 45◦.

Atsakymas: 45◦.

Kaip atrodo įprasta keturkampė prizmė? ir gavo geriausią atsakymą

Atsakymas iš Edit Piaf[guru]
Prizmė yra daugiakampis, kurio du paviršiai (prizmės pagrindai) yra lygūs daugiakampiai su atitinkamai lygiagrečiomis kraštinėmis, o likę paviršiai yra lygiagrečiai, kurių plokštumos lygiagrečios tiesei. Lygiagretainiai AabB, BbcC ir kt. vadinami šoniniais paviršiais; šonkauliai Aa, Bb, Cc ir kt. vadinami šoniniais šonkauliais. Prizmės aukštis yra bet koks statmenas, nukritęs iš bet kurio pagrindo taško į kito pagrindo plokštumą. Priklausomai nuo daugiakampio, esančio prie pagrindo, formos prizmė gali būti atitinkamai: trikampė, keturkampė, penkiakampė, šešiakampė ir kt. Jei prizmės šoninės briaunos yra statmenos pagrindo plokštumai, tai tokia prizmė yra vadinamas tiesiai; kitu atveju tai yra pasvirusi prizmė. Jei tiesios prizmės pagrindu yra taisyklingas daugiakampis, tai tokia prizmė dar vadinama taisyklingąja.
Taisyklinga prizmė yra tiesi prizmė, kurios pagrindas yra taisyklingas daugiakampis, tai šiuo atveju yra kvadratas.
Nubrėžiau tiesią prizmę, bet ji gali būti ir pasvirusi

Atsakymas iš Laiminga pabaiga[guru]
kubas

Atsakymas iš 3 atsakymai[guru]

Sveiki! Štai keletas temų su atsakymais į jūsų klausimą: kaip atrodo įprasta keturkampė prizmė?